题目内容
已知圆P:(x-m)2+(y-n)2=4与y轴交于A、B两点,且|
+
|=
,则|AB|=
.
| PA |
| PB |
| 10 |
| 6 |
| 6 |
分析:设点E是AB的中点,连结PE,由向量加法法则得向量
=
(
+
),结合题意算出|
|=
,即P到AB的距离等于
.然后在Rt△PAE中利用勾股定理算出AE长,即可得到|AB|的值.
| PE |
| 1 |
| 2 |
| PA |
| PB |
| PE |
| ||
| 2 |
| ||
| 2 |
解答:解: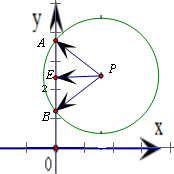 设点E是AB的中点,连结PE,则
设点E是AB的中点,连结PE,则
∵PE是△PAB的中线,
∴向量
=
(
+
)
又∵|
+
|=
,∴|
|=
∵⊙P中,E是弦AB的中点
∴PE⊥AB,可得|AE|=
=
=
因此,|AB|=2|AE|=
 设点E是AB的中点,连结PE,则
设点E是AB的中点,连结PE,则∵PE是△PAB的中线,
∴向量
| PE |
| 1 |
| 2 |
| PA |
| PB |
又∵|
| PA |
| PB |
| 10 |
| PE |
| ||
| 2 |
∵⊙P中,E是弦AB的中点
∴PE⊥AB,可得|AE|=
|
4-(
|
| ||
| 2 |
因此,|AB|=2|AE|=
| 6 |
点评:本题给出半径为2的圆P被y轴截得弦AB,在已知向量
+
长度的情况下求AB的长.着重考查了圆的标准方程、向量的加法法则和垂径定理等知识,属于中档题.
| PA |
| PB |

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目

 ,则|AB|= .
,则|AB|= .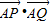 的取值范围.
的取值范围.