题目内容
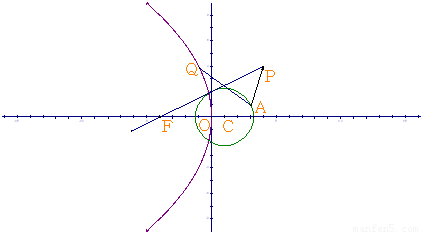
已知圆C:(x-m)2+y2=5(m<3)过点A(3,1),且过点P(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F.(1)求切线PF的方程;
(2)若抛物线E的焦点为F,顶点在原点,求抛物线E的方程.
(3)若Q为抛物线E上的一个动点,求
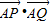 的取值范围.
的取值范围.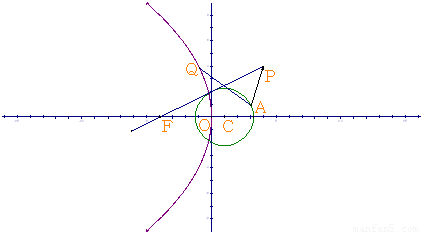
【答案】分析:(1)先将点A代入圆C方程,求得m的值,得到圆C的方程,再设直线PF的斜率为k,利用直线PF与圆C相切的几何性质求得k值,从而得到切线PF的方程;
(2)设抛物线标准方程为y2=-2px由焦点坐标求得p=8从而写出抛物线标准方程即可;
(3)设Q(x,y),分别求得向量的坐标,再利用向量的数量积得到 关于y的二次函数式,最后利用二次函数的性质即可求
关于y的二次函数式,最后利用二次函数的性质即可求 的取值范围.
的取值范围.
解答:解:(1)点A代入圆C方程,得(3-m)2+1=5.∵m<3,∴m=1.
圆C:(x-1)2+y2=5.设直线PF的斜率为k,则PF:y=k(x-4)+4,
即kx-y-4k+4=0.∵直线PF与圆C相切,∴ .解得
.解得 .
.
当k= 时,直线PF与x轴的交点横坐标为
时,直线PF与x轴的交点横坐标为 ,不合题意,舍去.
,不合题意,舍去.
当k= 时,直线PF与x轴的交点横坐标为-4,∴符合题意,∴直线PF的方程为y=
时,直线PF与x轴的交点横坐标为-4,∴符合题意,∴直线PF的方程为y= x+2…(6分)
x+2…(6分)
(2)设抛物线标准方程为y2=-2px,∵F(-4,0),∴p=8,∴抛物线标准方程为y2=-16x…(8分)
(3) ,设Q(x,y),
,设Q(x,y), ,
, .
.
∵y2=-16x,∴ .
.
∴ 的取值范围是(-∞,30].…(13分)
的取值范围是(-∞,30].…(13分)
点评:本小题主要考查直线的点斜式方程、抛物线的标准方程、抛物线的简单性质、平面向量数量积的运算等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
(2)设抛物线标准方程为y2=-2px由焦点坐标求得p=8从而写出抛物线标准方程即可;
(3)设Q(x,y),分别求得向量的坐标,再利用向量的数量积得到
 关于y的二次函数式,最后利用二次函数的性质即可求
关于y的二次函数式,最后利用二次函数的性质即可求 的取值范围.
的取值范围.解答:解:(1)点A代入圆C方程,得(3-m)2+1=5.∵m<3,∴m=1.
圆C:(x-1)2+y2=5.设直线PF的斜率为k,则PF:y=k(x-4)+4,
即kx-y-4k+4=0.∵直线PF与圆C相切,∴
 .解得
.解得 .
.当k=
 时,直线PF与x轴的交点横坐标为
时,直线PF与x轴的交点横坐标为 ,不合题意,舍去.
,不合题意,舍去.当k=
 时,直线PF与x轴的交点横坐标为-4,∴符合题意,∴直线PF的方程为y=
时,直线PF与x轴的交点横坐标为-4,∴符合题意,∴直线PF的方程为y= x+2…(6分)
x+2…(6分)(2)设抛物线标准方程为y2=-2px,∵F(-4,0),∴p=8,∴抛物线标准方程为y2=-16x…(8分)
(3)
 ,设Q(x,y),
,设Q(x,y), ,
, .
.∵y2=-16x,∴
 .
.∴
 的取值范围是(-∞,30].…(13分)
的取值范围是(-∞,30].…(13分)点评:本小题主要考查直线的点斜式方程、抛物线的标准方程、抛物线的简单性质、平面向量数量积的运算等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

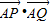 的取值范围.
的取值范围.