题目内容
已知椭圆 ,椭圆
,椭圆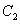 以
以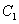 的长轴为短轴,且与
的长轴为短轴,且与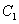 有相同的离心率。
有相同的离心率。
(1)求椭圆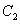 的方程;
的方程;
(2)设O为坐标原点,点A,B分别在椭圆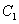 和
和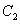 上,
上,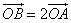 ,求直线
,求直线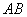 的方程。
的方程。
[来
【解析】(Ⅰ)由已知可设椭圆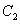 的方程为
的方程为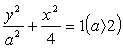 ,其离心率为
,其离心率为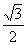 ,故
,故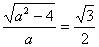 ,则
,则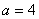 ,故椭圆
,故椭圆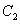 的方程为
的方程为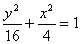 ------------4分
------------4分
(Ⅱ)解法一 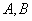 两点的坐标分别为
两点的坐标分别为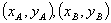 ,
,
由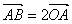 及(Ⅰ)知,
及(Ⅰ)知,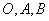 三点共线且点
三点共线且点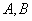 不在
不在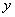 轴上,
轴上,
因此可设直线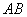 的方程为
的方程为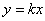 .------------6分
.------------6分
将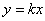 代入
代入 中,得
中,得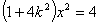 ,所以
,所以 ,
,
将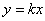 代入
代入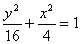 中,得
中,得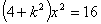 ,所以
,所以 ,------------8分
,------------8分
又由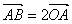 ,得
,得 ,即
,即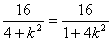 ,------------10分
,------------10分
解得 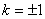 ,故直线
,故直线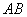 的方程为
的方程为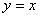 或
或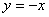 -------------12分
-------------12分
解法二 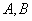 两点的坐标
两点的坐标 分别为
分别为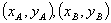 ,
,
 由
由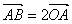 及(Ⅰ)知,
及(Ⅰ)知,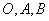 三点共线且点
三点共线且点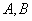 不在
不在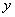 轴上,
轴上,
因此可设直线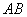 的方程为
的方程为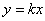 .
.
将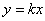 代入
代入 中,得
中,得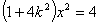 ,所以
,所以 ,
,
又由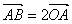 ,得
,得 ,
,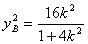 ,[来源:学_科_网Z_X_X_K]
,[来源:学_科_网Z_X_X_K]
将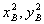 代入
代入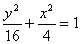 中,得
中,得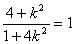 ,即
,即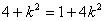 ,
,
解得 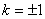 ,故直线
,故直线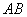 的方程为
的方程为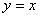 或
或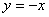

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
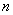 、抽测成绩的中位数及分数分别在
、抽测成绩的中位数及分数分别在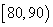 ,
,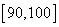 内的人数;
内的人数;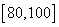 内的学生中任选两人进行调研谈话,求恰好有一人分数在
内的学生中任选两人进行调研谈话,求恰好有一人分数在
 满足约束条件
满足约束条件 ,则
,则 的最大值是 .
的最大值是 .  (B)
(B) 
 (D)
(D) 
 ,且a+b+c=1, 求证:a2+b2+c2≥
,且a+b+c=1, 求证:a2+b2+c2≥ .
. 中,抛物线
中,抛物线 上横坐标为1的点到其焦点的距离为 .
上横坐标为1的点到其焦点的距离为 . .
. ,由不等式
,由不等式 ,
, ,
, ,归纳得到推广结论:
,归纳得到推广结论:  ,则实数
,则实数
