题目内容
1．在直角坐标系中，曲线C的参数方程为$\left\{\begin{array}{l}x=2cosα\\ y=2sinα+2\end{array}\right.$，参数α∈[0，2π]．已知极坐标的极点在平面直角坐标系的原点O处，极轴与x轴的正半轴重合，且长度单位相同．直线l的极坐标方程为：$ρsin（θ-\frac{π}{3}）=5$．（1）求曲线C的直角坐标方程；
（2）求曲线C上任一点到直线l的距离的最大值．
分析 （1）利用三角函数的平方关系式，消去参数，即可得到直角坐标方程．
（2）求出直线的直角坐标方程，通过直线与圆的位置关系，圆心到直线的距离求解最值即可．
解答 解：（1）因为曲线C的参数方程为$\left\{\begin{array}{l}x=2cosα\\ y=2sinα+2\end{array}\right.$，参数α∈[0，2π]，
所以曲线C的直角坐标方程为x2+（y-2）2=4…（3分）
（2）∵$ρsin（θ-\frac{π}{3}）=5$
∴$\frac{1}{2}ρsinθ-\frac{{\sqrt{3}}}{2}ρcosθ=5$，即$ρsinθ-\sqrt{3}ρcosθ=10$
∴直线l的直角坐标方程为$\sqrt{3}x-y+10=0$…（6分）
由（1）知曲线C的方程为x2+（y-2）2=4，是（0，2）为圆心，半径为2的圆．
圆心到直线的距离$d=\frac{|-2+10|}{{\sqrt{{{（\sqrt{3}）}^2}+{1^2}}}}=4$，
圆与直线l相离，…（9分）
所以圆C上任一点到直线l的距离的最大值为4+2=6…（10分）
点评 本题考查圆的参数方程，直线的极坐标方程与普通方程的互化，直线与圆的位置关系的应用，考查计算能力．
练习册系列答案
相关题目
12．袋中有10个外形相同的球，其中5个白球，3个黑球，2个红球，从中任意取出一球，已知它不是白球，则它是黑球的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{3}{10}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{5}$ |
9．焦点分别为（-2，0），（2，0）且经过点（2，3）的双曲线的标准方程为（ ）
| A． | x2-$\frac{{y}^{2}}{3}$=1 | B． | $\frac{{x}^{2}}{3}-{y}^{2}=1$ | C． | y2-$\frac{{x}^{2}}{3}$=1 | D． | $\frac{{x}^{2}}{2}-\frac{{y}^{2}}{2}=1$ |
16．下列各组函数中，表示同一函数的是（ ）
| A． | $y=x+1与y=\frac{{{x^2}+x}}{x}$ | B． | $f（x）=\frac{x^2}{{{{（{\sqrt{x}}）}^2}}}与g（x）=x$ | ||
| C． | $f（x）=x\frac{|x|}{x}与f（t）=\left\{\begin{array}{l}t（t＞0）\\-t（t＜0）\end{array}\right.$ | D． | $f（x）=|x|与g（x）=\left\{\begin{array}{l}x（x＞0）\\-x（x＜0）\end{array}\right.$ |
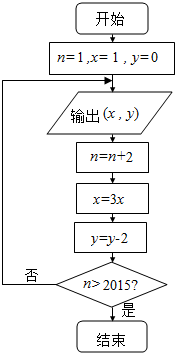某算法的流程图如图所示，记输出的数组（x，y）依次为（x1，y1），（x2，y2），…（x3，y3）…，若程序运行中输出的一个数组是（9，y），则y=-4；程序结束时，共输出（x，y）的组数为1008．