题目内容
已知各项均为正整数的数列{an}满足a1<4,an+1=2an+1,且
<
对任意n∈N﹡恒成立.数列{an},{bn}满足等式2(λn+bn)=2nλn+an+1(λ>0).
(1)求证数列{ an+l}是等比数列,并求出{an}的通项公式;
(2)求数列{bn}的前n项和Sn;
(3)证明存在k∈N﹡,使得
≤
对任意n∈N﹡均成立.
| n |
 |
| i=1 |
| 1 |
| 1+ai |
| 1 |
| 2 |
(1)求证数列{ an+l}是等比数列,并求出{an}的通项公式;
(2)求数列{bn}的前n项和Sn;
(3)证明存在k∈N﹡,使得
| bn+1 |
| bn |
| bk+1 |
| bk |
分析:(1)由an+1=2an+1得:an+1+1=2(an+1),由a1>0,a1+1>1,知{an+1}是等比数列,由
<
,知
<
,由此能求出{an}的通项公式.
(2)由2(λn+bn)=2nλn+an+1(λ>0)得:bn=(n-1)λn+2n.设数列{(n-1)λn}的前n项的和为Tn,Tn=λ2+2λ3+3λ4+…+(n-1)λnλTn=λ3+2λ4+…+(n-2)λn+(n-1)λn+1(1-λ)Tn=λ2+λ3+λ4+…+λn-(n-1)λn+1,由此能求出数列{bn}的前n项和.
(3)存在k=1满足题意
≤
?2n•λn+1≤(n-1)λn+2+4(n-1)λn+2nλ2.由此能够推导出存在k∈N﹡,使得
≤
对任意n∈N﹡均成立.
| n |
 |
| i=1 |
| 1 |
| 1+ai |
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
(2)由2(λn+bn)=2nλn+an+1(λ>0)得:bn=(n-1)λn+2n.设数列{(n-1)λn}的前n项的和为Tn,Tn=λ2+2λ3+3λ4+…+(n-1)λnλTn=λ3+2λ4+…+(n-2)λn+(n-1)λn+1(1-λ)Tn=λ2+λ3+λ4+…+λn-(n-1)λn+1,由此能求出数列{bn}的前n项和.
(3)存在k=1满足题意
| nλn+1+2n+1 |
| (n-1)λn+2n |
| λ2+22 |
| 2 |
| bn+1 |
| bn |
| bk+1 |
| bk |
解答:解:(1)由an+1=2an+1得:an+1+1=2(an+1),
∵a1>0,
∴a1+1>1,
∴{an+1}是等比数列,首项为a1+1,公比q=2.
∵
<
,
∴
<
,
即
<
•
对任意n∈N*恒成立,
∴
<4,
∴a1≥3.
∵a1<4,a1∈N*,
∴a1=3.
∴等比数列{an+1}的首项为a1+1=3+1=4,公比q=2.
∴an+1=4•2n-1,即an=4•2n-1-1=2n+1-1.
即{an}的通项公式是an=2n+1-1,n≥1.
(2)由2(λn+bn)=2nλn+an+1(λ>0),
得:bn=(n-1)λn+2n
设数列{(n-1)λn}的前n项的和为Tn
∴Tn=λ2+2λ3+3λ4+…+(n-1)λnλTn
=λ3+2λ4+…+(n-2)λn+(n-1)λn+1(1-λ)Tn
=λ2+λ3+λ4+…+λn-(n-1)λn+1
当λ=1时,Tn=1+2+…+(n-1)=
当λ≠1时,Tn=
,
∴Sn=
.
(3)存在k=1满足题意
≤
?2n•λn+1
≤(n-1)λn+2+4(n-1)λn+2nλ2(*)
当n≥2时,∵(n-1)λn+2+4(n-1)λn+2nλ2
=(n-1)λn(λ2+4)+2nλ2
≥(n-1)λn•4λ+2nλ2>(4n-4)λn+1
≥2nλn+1
又n=1时,(*)式成立∴对任意n∈N*,(*)式成立.
∵a1>0,
∴a1+1>1,
∴{an+1}是等比数列,首项为a1+1,公比q=2.
∵
| n |
 |
| i=1 |
| 1 |
| 1+ai |
| 1 |
| 2 |
∴
| ||||
1-
|
| 1 |
| 2 |
即
| 1 |
| 1+a1 |
| 1 |
| 4 |
| 1 | ||
1-
|
∴
| 1 |
| 1+a1 |
∴a1≥3.
∵a1<4,a1∈N*,
∴a1=3.
∴等比数列{an+1}的首项为a1+1=3+1=4,公比q=2.
∴an+1=4•2n-1,即an=4•2n-1-1=2n+1-1.
即{an}的通项公式是an=2n+1-1,n≥1.
(2)由2(λn+bn)=2nλn+an+1(λ>0),
得:bn=(n-1)λn+2n
设数列{(n-1)λn}的前n项的和为Tn
∴Tn=λ2+2λ3+3λ4+…+(n-1)λnλTn
=λ3+2λ4+…+(n-2)λn+(n-1)λn+1(1-λ)Tn
=λ2+λ3+λ4+…+λn-(n-1)λn+1
当λ=1时,Tn=1+2+…+(n-1)=
| n(n-1) |
| 2 |
当λ≠1时,Tn=
| λ2-λn+1-(n-1)(1-λ)λn+1 |
| (1-λ)2 |
∴Sn=
|
(3)存在k=1满足题意
| nλn+1+2n+1 |
| (n-1)λn+2n |
| λ2+22 |
| 2 |
≤(n-1)λn+2+4(n-1)λn+2nλ2(*)
当n≥2时,∵(n-1)λn+2+4(n-1)λn+2nλ2
=(n-1)λn(λ2+4)+2nλ2
≥(n-1)λn•4λ+2nλ2>(4n-4)λn+1
≥2nλn+1
又n=1时,(*)式成立∴对任意n∈N*,(*)式成立.
点评:本题考查数列与不等式的综合运算,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
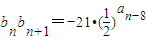 ,且b1=192,其前n项积为Tn,试问n为何值时,Tn取得最大值?
,且b1=192,其前n项积为Tn,试问n为何值时,Tn取得最大值?