题目内容
18.“k=1”是“直线y=x+k与圆x2+y2=1相交”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 由k=1时直线与圆相交,判断充分性成立;由直线与圆相交时求出k的取值范围,判断必要性不成立;可得结论.
解答 解:k=1时,直线为x-y+1=0,圆x2+y2=1的圆心O到直线的距离为d=$\frac{1}{\sqrt{2}}$<1,
直线与圆相交,充分性成立;
直线y=x+k与圆x2+y2=1相交时,圆心到直线的距离d=$\frac{|k|}{\sqrt{2}}$<1,
解得k∈(-$\sqrt{2}$,$\sqrt{2}$),必要性不成立;
所以“k=1”是“直线y=x+k与圆x2+y2=1相交”的充分不必要条件.
故选:A.
点评 本题考查了直线与圆的位置关系以及充分与必要条件的判断问题,是基础题目.

练习册系列答案
相关题目
8.长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,则异面直线BC1与AC所成角的余弦值为( )
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{1}{2}$ |
9.已知数列{an}满足:a1=$\frac{3}{8}$,an+2-an≤3n,an+6-an≥91•3n,则a2015=( )
| A. | $\frac{{3}^{2015}}{2}$+$\frac{3}{2}$ | B. | $\frac{{3}^{2015}}{8}$ | C. | $\frac{{3}^{2015}}{8}$+$\frac{3}{2}$ | D. | $\frac{{3}^{2015}}{2}$ |
10.函数f(x)=x3-x+2在下列区间内一定存在零点的是( )
| A. | (1,2) | B. | (0,1) | C. | (-2,-1) | D. | (-1,0) |
8.若双曲线$\frac{x^2}{4}-\frac{y^2}{5}=1$与椭圆$\frac{x^2}{a^2}+\frac{y^2}{16}=1$有共同的焦点,且a>0,则a的值为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | $\sqrt{15}$ | D. | $\sqrt{17}$ |
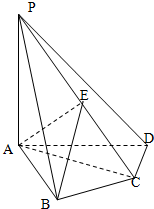 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.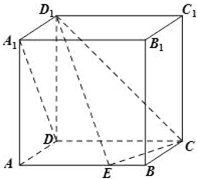 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.