题目内容
△ABC中角A，B，C所对的边分别是a，b，c，若a2+b2-c2=
ab，则角C为（ ）
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
考点：余弦定理
专题：计算题,解三角形
分析：利用余弦定理表示出cosC，把已知的等式代入求出cosC的值，由C为三角形的内角，利用特殊角的三角函数值即可求出C的度数．
解答：
解：∵a2+b2-c2=
ab，
∴根据余弦定理得：cosC=
=
，
又∵C为三角形的内角，
则∠C=30°．
故选：A．
| 3 |
∴根据余弦定理得：cosC=
| a2+b2-c2 |
| 2ab |
| ||
| 2 |
又∵C为三角形的内角，
则∠C=30°．
故选：A．
点评：此题考查了余弦定理，以及特殊角的三角函数值，利用了整体代入的思想，余弦定理很好的建立了三角形的边角关系，熟练掌握余弦定理是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
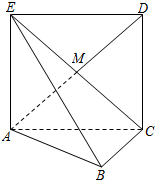如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC⊥BC，且AC=BC．
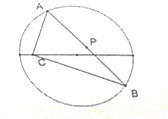已知x2+y2=a2，定点C（c，0）．（a＞0，c≠a）．AB为圆上的动点∠ACB=90°．求AB中点P的轨迹方程．在△ABC中，a=2，b=2
，B=45°，则A等于（ ）
| 2 |
| A、30° |
| B、60° |
| C、60°或120° |
| D、30°或150° |
某超市对某商品开展为期两天的抽奖促销活动，第一天的活动方案为：顾客转动如图所示圆盘，当指针指向阴影部分（图中四个阴影部分均为扇形，且每个扇形圆心角均为15°，边界忽略不计）即为中奖．已知集合A={1，2，3}，B={3，6，7}，则A∪B等于（ ）
| A、{3} |
| B、{3，4} |
| C、{1，2，3，6，7} |
| D、∅ |