题目内容
已知向量: =(cosωx-sinωx,2sinωx),(其中ω>0),函数f(x)=
=(cosωx-sinωx,2sinωx),(其中ω>0),函数f(x)= ,若f(x)相邻两对称轴间的距离为
,若f(x)相邻两对称轴间的距离为 .
.
(1)求ω的值,并求f(x)的最大值及相应x的集合;
(2)在△ABC中,a,b,c分别是A,B,C所对的边,△ABC的面积S=5 ,b=4,f(A)=1,求边a的长.
,b=4,f(A)=1,求边a的长.
解:(1)∵f(x)=cos2ωx-sin2ωx+2 sin2ωx
sin2ωx
=
又题意可得T=π,∴ω=1,∴f(x)=2sin
当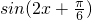 =1时,f(x)有最大值为2,
=1时,f(x)有最大值为2,
∴x∈
(2)∵f(A)=2sin(2A+ )=1
)=1
∴sin(2A+ )=
)=
∵0<A<π
∴2A+
S= bcsin
bcsin =5
=5 c=5
c=5
由余弦定理得:a2=16+25-2×4×5cos =21∴a=
=21∴a= .
.
分析:(1)先根据二倍角公式和两角和与差的正弦公式进行化简,再由最小正周期得到w的值,从而可确定函数f(x)的解析式,然后再由正弦函数的最值可求得f(x)的最大值及相应x的集合.
(2)将A代入可确定A的值,再由三角形的面积公式可得到c的值,最后根据余弦定理可求得a的值.
点评:本题主要考查二倍角公式、两角和与差的公式的应用,考查正弦函数的基本性质--最值、周期性.三角函数是高考的重点内容,一般以基础题为主,要强化基础的夯实.
 sin2ωx
sin2ωx=

又题意可得T=π,∴ω=1,∴f(x)=2sin

当
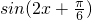 =1时,f(x)有最大值为2,
=1时,f(x)有最大值为2,∴x∈

(2)∵f(A)=2sin(2A+
 )=1
)=1∴sin(2A+
 )=
)=
∵0<A<π
∴2A+

S=
 bcsin
bcsin =5
=5 c=5
c=5由余弦定理得:a2=16+25-2×4×5cos
 =21∴a=
=21∴a= .
.分析:(1)先根据二倍角公式和两角和与差的正弦公式进行化简,再由最小正周期得到w的值,从而可确定函数f(x)的解析式,然后再由正弦函数的最值可求得f(x)的最大值及相应x的集合.
(2)将A代入可确定A的值,再由三角形的面积公式可得到c的值,最后根据余弦定理可求得a的值.
点评:本题主要考查二倍角公式、两角和与差的公式的应用,考查正弦函数的基本性质--最值、周期性.三角函数是高考的重点内容,一般以基础题为主,要强化基础的夯实.

练习册系列答案
相关题目