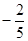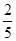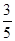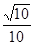题目内容
如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( )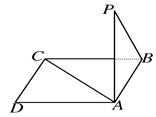
| A.90° | B.60° |
| C.45° | D.30° |
B
解析试题分析:连接BD交AC于点O,取PD中点Q,连接OQ,所以OQ//PB,
设正方形ABCD边长为a,因为PA垂直平面ABCD,PA=AB,所以PD=PB=DB=AC= ,
,
因为在三角形DBP中,O、Q是中点,所以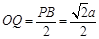 ,在直角三角形PAD中,
,在直角三角形PAD中,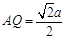 , 而
, 而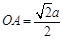 ,所以三角形AOQ是等边三角形,即三个角都是60度,所以OQ与AC所成的角=60度, 因为OQ||PB,所以PB与AC所成的角为60°.
,所以三角形AOQ是等边三角形,即三个角都是60度,所以OQ与AC所成的角=60度, 因为OQ||PB,所以PB与AC所成的角为60°.
考点:本小题主要考查两条异面直线的夹角.
点评:要求两条异面直线的夹角,需要先做出两条异面直线的夹角再求解,注意两条异面直线的夹角的取值范围。

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案用M表示平面, 表示一条直线,则M内至少有一直线与
表示一条直线,则M内至少有一直线与 ( )
( )
| A.平行; | B.相交; | C.异面; | D.垂直。 |
如图,三棱锥 底面为正三角形,侧面
底面为正三角形,侧面 与底面垂直且
与底面垂直且 ,已知其主视图的面积为
,已知其主视图的面积为 ,则其左视图的面积为
,则其左视图的面积为
A. | B. | C. | D. |
已知长方体ABCD—A1B1ClD1内接于球O,底面ABCD是边长为2的正方形,E为AA1的中点,OA⊥平面BDE,则球O的表面积为
A.8 | B.16 : : | C.14 | D.18 |
设、 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若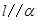 , , ,则 ,则 | D.若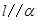 , , ,则 ,则 |
如图,四面体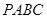 的六条边均相等,
的六条边均相等,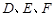 分别是
分别是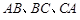 的中点,则下列四个结论中不成立的是 ( )
的中点,则下列四个结论中不成立的是 ( ) 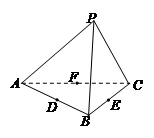
A.平面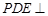 平面 平面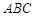 | B.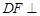 平面 平面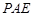 |
C. //平面 //平面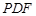 | D.平面 平面 平面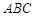 |
设 是平面
是平面 内的一条定直线,
内的一条定直线, 是平面
是平面 外的一个定点,动直线
外的一个定点,动直线 经过点
经过点 且与
且与 成
成 角,则直线
角,则直线 与平面
与平面 的交点
的交点 的轨迹是
的轨迹是
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
设m,n是异面直线,则(1)一定存在平面α,使m α,且n∥α;(2)一定存在平面α,使m
α,且n∥α;(2)一定存在平面α,使m α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距离相等;(4)一定存在无数对平面α和β,使m
α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距离相等;(4)一定存在无数对平面α和β,使m α,n
α,n β且α⊥β。上述4个命题中正确命题的序号是( )
β且α⊥β。上述4个命题中正确命题的序号是( )
| A.(1)(2)(3) | B.(1)(2)(4) | C.(1)(3)(4) | D.(1)(4) |