Question

已知椭圆的中心在原点，焦点F₁，F₂在x轴上，且椭圆的长轴与短轴长之比为3：2．已知椭圆上一动点P，满足．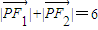
（1）求椭圆的方程；
（2）若，求△PF₁F₂的面积；
（3）过点P（1，1）的直线与椭圆交于C、D两点，且满足，求直线CD的方程．

Answer 1

【答案】分析：（1）由椭圆的定义及已知条件，求出a、b 的值，依据条件写出标准方程．
（2）由题意知，△PF₁F₂为直角三角形，由勾股定理和椭圆的第一定义建立方程组，求出直角三角形两直角边的积，
从而求出△PF₁F₂的面积．
（3）点斜式设出直线CD的方程代入椭圆的方程，转化为关于x的一元二次方程，由知，点P为CD的中点，
故方程的两根之和等于2，求出斜率，即得直线CD的方程．
解答：解：（1）由椭圆的定义知，2a=6，2a：2b=3：2，b=2，故所求的椭圆方程为 ；
（2）⇒|PF₁||PF₂|=8，，
所以，所求面积为4；
（3）椭圆方程为 ，设弦CD的斜率为k，
则CD：y=k（x-1）+1=kx+1-k，
代入椭圆方程，得4x²+9（kx+1-k）²-36=0，
即（4+9k²）x²+18k（1-k）x+9（1-k）²-36=0，由知，点P为CD的中点，
故方程的两根之和等于2，由，解得，此时△＞0，
故所求直线CD的方程为4x+9y-13=0．
点评：本题考查椭圆的定义和标准方程的求法，直线和圆锥曲线的位置关系、一元二次方程根与系数的关系．