题目内容
已知 .
.
(1)求f(x)的周期和单调减区间;
(2)设A为锐角三角形的内角,且 ,求tanA的值.
,求tanA的值.
解:(1)因为
=(sin2x+cos2x)2-2sin2xcos2x+sinxcosx(2sin2x-1)-
=
=
=
= .
.
∴f(x)的周期为: ,
,
因为 ,
,
所以
函数的单调减区间为 .
.
(2)由f(A)= ,得
,得
∵0
∴ ,
, ,
,
 .
.
于是tan2A=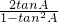 =-1,
=-1,
解得tanA=1+ 或tanA=1-
或tanA=1- ,
,
因为tanA>0,
∴tanA=1+ .
.
分析:(1)通过配方利用平方关系式、二倍角公式,然后利用两角和的余弦函数,化简函数为一个角的一个三角函数的形式,即可求f(x)的周期和单调减区间;
(2)设A为锐角三角形的内角,利用 ,结合A的范围求出A的值,然后求出tanA的值.
,结合A的范围求出A的值,然后求出tanA的值.
点评:本题是中档题,考查三角函数的化简求值,平方关系式,二倍角公式,两角和的余弦函数的应用,考查计算能力.

=(sin2x+cos2x)2-2sin2xcos2x+sinxcosx(2sin2x-1)-

=

=

=

=
 .
.∴f(x)的周期为:
 ,
,因为
 ,
,所以

函数的单调减区间为
 .
.(2)由f(A)=
 ,得
,得
∵0

∴
 ,
, ,
, .
.于是tan2A=
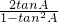 =-1,
=-1,解得tanA=1+
 或tanA=1-
或tanA=1- ,
,因为tanA>0,
∴tanA=1+
 .
.分析:(1)通过配方利用平方关系式、二倍角公式,然后利用两角和的余弦函数,化简函数为一个角的一个三角函数的形式,即可求f(x)的周期和单调减区间;
(2)设A为锐角三角形的内角,利用
 ,结合A的范围求出A的值,然后求出tanA的值.
,结合A的范围求出A的值,然后求出tanA的值.点评:本题是中档题,考查三角函数的化简求值,平方关系式,二倍角公式,两角和的余弦函数的应用,考查计算能力.

练习册系列答案
相关题目
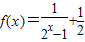
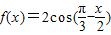
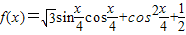 .
.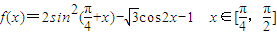
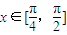 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.