题目内容
已知△ABC内角A,B,C的对边分别是a,b,c,若cos B=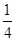 ,b=2,sin C=2sin A,则△ABC的面积为( ).
,b=2,sin C=2sin A,则△ABC的面积为( ).
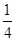 ,b=2,sin C=2sin A,则△ABC的面积为( ).
,b=2,sin C=2sin A,则△ABC的面积为( ).A.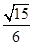 | B.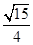 | C.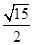 | D.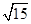 |
B
由正弦定理 ,得c=2a①
,得c=2a①
由余弦定理b2=a2+c2-2accos B,得4=a2+c2-2ac×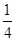 ②
②
由①②得:a=1,c=2,又sin B= =
=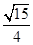 .所以S△ABC=
.所以S△ABC= acsin B=
acsin B= ×1×2×
×1×2×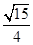 =
=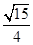
 ,得c=2a①
,得c=2a①由余弦定理b2=a2+c2-2accos B,得4=a2+c2-2ac×
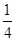 ②
②由①②得:a=1,c=2,又sin B=
 =
=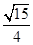 .所以S△ABC=
.所以S△ABC= acsin B=
acsin B= ×1×2×
×1×2×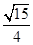 =
=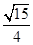

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
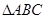 中,内角
中,内角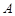 ,
,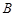 ,
,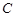 的对边分别为
的对边分别为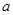 ,
,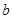 ,
,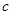 ,且
,且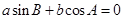 .
.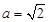 ,
,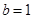 ,求
,求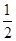
 cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=- .
. ,b=5,求向量
,b=5,求向量 在
在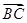 方向上的投影.
方向上的投影.

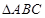 的内角
的内角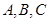 所对边的长分别为
所对边的长分别为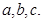 若
若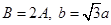 ,则角
,则角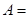 ( )
( )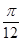
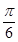
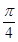
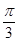
 ,cos B=
,cos B=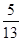 ,b=3,则c=________.
,b=3,则c=________. 中,
中, ,
, ,
, ,则
,则 ____________.
____________.