题目内容
已知定义域为 的函数
的函数 是奇函数。
是奇函数。
(Ⅰ)求 的值;
的值;
(Ⅱ)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;
【答案】
(1)a=2;(2)
【解析】
试题分析:(1)因为f(x)是奇函数,所以f(0)=0,即 ,解得b=1,
,解得b=1,
从而有f(x)= 。又由f(1)=-f(-1)知
。又由f(1)=-f(-1)知 ,解得a=2
,解得a=2
(2)由(1)知f(x)= =
=
由上式易知f(x)在 上为减函数。
上为减函数。
又因f(x)为奇函数,从而不等式 等价于
等价于

因f(x)为减函数,由上式推得 
即对一切 有
有 从而判别式
从而判别式 ,解得
,解得
考点:本题主要考查函数的奇偶性,函数解析式求法,指数运算,抽象不等式解法。
点评:中档题,研究函数的奇偶性,应先确定函数的定义域是否关于原点对称,其次,再研究f(-x)与f(x)d 关系。涉及抽象不等式问题,往往利用函数的单调性,转化成具体不等式求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
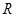 的函数
的函数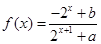 是奇函数。
是奇函数。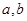 的值;
的值;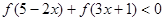
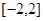 的函数
的函数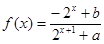 是奇函数.
是奇函数.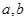 的值; (Ⅱ)解关于
的值; (Ⅱ)解关于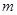 的不等式
的不等式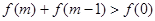 .
.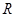 的函数
的函数 是奇函数.
是奇函数. 的值;
的值;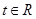 ,不等式
,不等式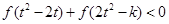 恒成立,求
恒成立,求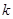 的取值范围.
的取值范围.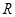 的函数
的函数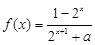 是奇函数.
是奇函数.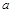 的值;
的值;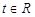 ,不等式
,不等式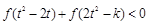 恒成立,求实数
恒成立,求实数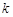 的取值范围.
的取值范围. 的函数
的函数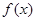 是偶函数,当
是偶函数,当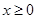 时,
时,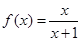 .
.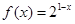 在区间
在区间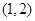 上有解
上有解