题目内容
设常数a>0,对x1,x2∈R,P(x,y)是平面上任意一点,定义运算“?”:x1?x2=(x1+x2)2-(x1-x2)2,d1(P)=| 1 |
| 2 |
| x?x+y?y |
| 1 |
| 2 |
| (x-a)?(x-a) |
(1)若x≥0,求动点P(x,
| x?a |
(2)计算d1(P)和d2(P),并说明其几何意义;
(3)在(1)中的轨迹C中,是否存在两点A1,A2,使之满足d1(A1)=
| a |
| a |
分析:(1)由新定义运算“?”:x1?x2=(x1+x2)2-(x1-x2)2,,化简
即可求得;(2)利用新定义运算进行化简,借助于函数关系说明其几何意义;(3)把探索型命题转化为封闭型命题求解.
| x?a |
解答:解:(1)由y=
=
=
,
可知:y2=4ax(x≥0,y≥0),所以轨迹C为抛物线y2=4ax(x≥0,y≥0)在第一象限内的部分(包括原点);
(2)d1(P)=
=
=
,
d2(P)=
=|x-a|,
分别表示P点到原点和到直线x=a的距离;
(3)设若存在为A1(x1,y1)A2(x2,y2),则由d1(A1)=
d2(A1)且d1(A2)=
d2(A2)
得
,即
,即
,
所以x1、x2是方程(a-1)x2-(4a+2a2)x+a3=0的两个根.…2分
要使A1,A2存在,必须
<br/>,即
,所以必须a>1
当a>1时,由于(x1-a)(x2-a)=x1x2-a(x1+x2)+a2=
-a
+a2=
=
=
<0,即x1-a与x2-a异号.
所以d1(A1)+d1(A2)=
(|x1-a|+|x2-a|)=
|(x1-a)-(x2-a)|=
=
.…2分
| x?a |
| (x+a)2-(x-a)2 |
| 4ax |
可知:y2=4ax(x≥0,y≥0),所以轨迹C为抛物线y2=4ax(x≥0,y≥0)在第一象限内的部分(包括原点);
(2)d1(P)=
| 1 |
| 2 |
| x?x+y?y |
| 1 |
| 2 |
| 4x2+4y2 |
| x2+y2 |
d2(P)=
| 1 |
| 2 |
| 4(x-a)2 |
分别表示P点到原点和到直线x=a的距离;
(3)设若存在为A1(x1,y1)A2(x2,y2),则由d1(A1)=
| a |
| a |
得
|
|
|
所以x1、x2是方程(a-1)x2-(4a+2a2)x+a3=0的两个根.…2分
要使A1,A2存在,必须
|
|
当a>1时,由于(x1-a)(x2-a)=x1x2-a(x1+x2)+a2=
| a3 |
| a-1 |
| 4a+2a2 |
| a-1 |
=
| a3-4a2-2a3+a3-a2 |
| a-1 |
| -5a2 |
| a-1 |
所以d1(A1)+d1(A2)=
| a |
| a |
| a |
|
=
2a
| ||
| a-1 |
| 5a+4 |
点评:本题是新定义运算题,解题的关键是理解新定义运算,并进行化简.探索型问题通常是假设存在转化为封闭型命题解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
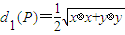 ,
,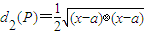 .
.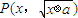 的轨迹C;
的轨迹C;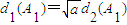 且
且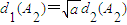 ?若存在,求出a的取值范围,并请求出d1(A1)+d1(A2)的值;若不存在,请说明理由.
?若存在,求出a的取值范围,并请求出d1(A1)+d1(A2)的值;若不存在,请说明理由.