题目内容
在双曲线
-
=1的右支上求一点 P,使它到左焦点的距离是它到右准线距离的4倍.
| x2 |
| 4 |
| y2 |
| 12 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出双曲线的a,b,c,e,及右准线方程,设P(m,n)到右准线距离为d,运用双曲线的第二定义,得到P到右焦点的距离为2d,由条件可得,d=2,再由点到直线的距离公式可得m=3,代入双曲线方程,解得n,进而得到P的坐标.
解答:
解:双曲线
-
=1的a=2,b=2
,
则c=
=4,e=
=2,右准线方程为x=
,即有x=1,
设P(m,n)到右准线距离为d,
根据第二定义,可得P到右焦点的距离为ed,
∵右支上一点P到左焦点的距离是到右准线距离的4倍,
∴P到左焦点的距离为4d,
∴4d-ed=2a=4,
∴d=
=
=2,即m-1=2,解得m=3,
则n2=12×(
-1)=15,即有n=±
.
则所求P的坐标为(3,±
).
| x2 |
| 4 |
| y2 |
| 12 |
| 3 |
则c=
| 4+12 |
| c |
| a |
| a2 |
| c |
设P(m,n)到右准线距离为d,
根据第二定义,可得P到右焦点的距离为ed,
∵右支上一点P到左焦点的距离是到右准线距离的4倍,
∴P到左焦点的距离为4d,
∴4d-ed=2a=4,
∴d=
| 4 |
| 4-e |
| 4 |
| 2 |
则n2=12×(
| 9 |
| 4 |
| 15 |
则所求P的坐标为(3,±
| 15 |
点评:本题考查双曲线的定义,考查双曲线的几何性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
对任意两个正整数x,y,定义某种新运算?,当x,y都为正偶数或者为正奇数时:x?y=x+y;当x,y中有一个为正奇数,另一个为正偶数时:x?y=xy.则在上述定义下,集合M={(m,n)|m?n=36,m,n∈N* }中元素的个数是( )
| A、6 | B、35 | C、36 | D、41 |
已知某线性规划问题的约束条件是
,则下列目标函数中,在点(3,1)处取得最小值的是( )
|
| A、z=2x-y | ||
| B、z=-2x+y | ||
C、z=-
| ||
| D、z=2x+y |
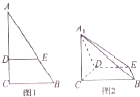 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到A1DE的位置,使A2C⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到A1DE的位置,使A2C⊥CD,如图2.