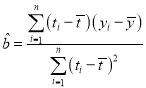题目内容
【题目】如图,四棱锥![]() 的底面
的底面![]() 是直角梯形,
是直角梯形,![]() ,
, ![]() ,
,![]() ,
,![]() , 且
, 且![]() ,
,![]() ,
,![]()
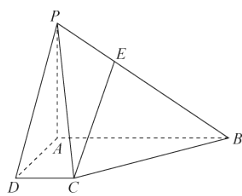
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离;
的距离;
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 的三等分点
的三等分点![]() ,法一,利用线面平行的判定定理证明.法二,利用面面平行判定定理证明;
,法一,利用线面平行的判定定理证明.法二,利用面面平行判定定理证明;
(2)法一,利用等积转换即![]() ,即可求得,法二,利用空间向量法,求点到面的距离.
,即可求得,法二,利用空间向量法,求点到面的距离.
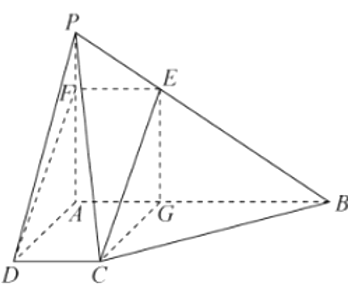
(1)解法一:取![]() 的三等分点
的三等分点![]() ,连结
,连结![]() ,则
,则![]()
又因为![]() ,所以
,所以![]() 且
且![]() ,
,
因为![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,
,
四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,
,
又平面![]() 平面
平面 ![]() ,
,![]() 平面
平面 ![]() ,
,
所以![]() 平面
平面 ![]() .
.
解法二:取![]() 的三等分点
的三等分点![]() ,连结
,连结![]() ,则
,则![]() ,
,
又因为![]() ,
,
所以![]() 且
且![]() ,
,![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
因为![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,
,
四边形![]() 是平行四边形.
是平行四边形.
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又因为![]() ,
,![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解法一:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以,![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
点![]() 平面
平面![]() 的距离是
的距离是![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
因为![]() ,所以,
,所以,![]()
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法二:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
因为![]() ,
,![]() ,所以
,所以![]()
所以,![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
分别以![]() 为
为![]() 轴
轴![]() 轴
轴![]() 轴,建立空间坐标系,
轴,建立空间坐标系,
![]() ’
’![]() ,
,
设平面![]() 法向量
法向量![]() ,
,
因为 ,所以
,所以![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() , 则
, 则
点![]() 到平面
到平面![]() 的距离
的距离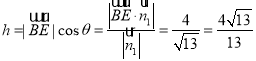 ,
,
点![]() 到平面
到平面![]() 的距离为
的距离为 ![]() .
.

【题目】微信是现代生活信息交流的重要工具,随机对使用微信的![]() 人进行统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信依赖”,不超过
人进行统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信依赖”,不超过![]() 两小时的人被定义为“非微信依赖”,已知“非微信依赖”与“微信依赖”人数比恰为
两小时的人被定义为“非微信依赖”,已知“非微信依赖”与“微信依赖”人数比恰为![]() .
.
使用微信时间(单位:小时) | 频数 | 频率 |
| 5 | 0.05 |
| 15 | 0.15 |
| 15 | 0.15 |
|
|
|
| 30 | 0.30 |
|
|
|
合计 | 100 | 1.00 |
(1)确定![]() 的值;
的值;
(2)为进一步了解使用微信对自己的日常工作和生活是否有影响,从“微信依赖”和“非微信依赖”![]() 人中用分层抽样的方法确定
人中用分层抽样的方法确定![]() 人,若需从这
人,若需从这![]() 人中随机选取
人中随机选取![]() 人进行问卷调查,设选取的
人进行问卷调查,设选取的![]() 人中“微信依赖”的人数为
人中“微信依赖”的人数为![]() ,求
,求![]() 的分布列;
的分布列;
(3)求选取的![]() 人中“微信依赖”至少
人中“微信依赖”至少![]() 人的概率.
人的概率.