题目内容
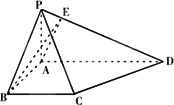
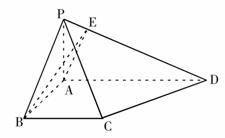
如图,在四棱柱P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
(I)当正视方向与向量
的方向相同时,画出四棱锥P-ABCD的正视图(要求标出尺寸,并写出演算过程);
(II)若M为PA的中点,求证:DM∥平面PBC;
(III)求三棱锥D-PBC的体积.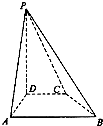
(I)当正视方向与向量
| AD |
(II)若M为PA的中点,求证:DM∥平面PBC;
(III)求三棱锥D-PBC的体积.



(I)在梯形ABCD中,作CE⊥AB,E为垂足,则四边形ADCE为矩形,∴AE=CD=3.
直角三角形BCE中,∵BC=5,CE=AD=4,由勾股定理求得BE=3,∴AB=6.
在直角三角形PAD中,∵∠PAD=60°,AD=4,∴PD=AD•tan60°=4
| 3 |
(II)∵M为PA的中点,取PB得中点为N,则MN平行且等于
| 1 |
| 2 |
| 1 |
| 2 |
故MNCD为平行四边形,故DM∥CN.
由于DM 不在平面PBC内,而CN在平面PBC内,故DM∥平面PBC.
(III)三棱锥D-PBC的体积VD-PBC=VP-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 4(3+6) |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |

练习册系列答案
相关题目
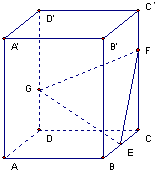 如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求:
如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求: 如图,在四棱柱P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=
如图,在四棱柱P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=