题目内容
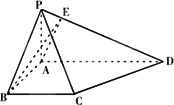
如图,在四棱柱P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥平面ABCD,PD与平面ABCD成30°角.
(Ⅰ)若AE⊥PD,E为垂足,求证:BE⊥PD;
(Ⅱ)求平面PAB与平面PCD所成锐二面角的余弦值.

【答案】分析:(Ⅰ)欲证直线与直线垂直,可先证直线与平面垂直,即PD⊥平面BAE,利用线面垂直的判定,需寻找线线垂直,故可证.
(Ⅱ)利用空间向量,构建空间直角坐标系,分别求出平面PAB与平面PCD的法向量,从而可求平面PAB与平面PCD所成锐二面角的余弦值.
解答: (Ⅰ)证明:∵∠BAD=90°,∴BA⊥AD
(Ⅰ)证明:∵∠BAD=90°,∴BA⊥AD
∵PA⊥底面ABCD,BA?底面ABCD
∴BA⊥PA.
∵PA∩AD=A,
∴BA⊥平面PAD.
∵PD?平面PAD.
∴PD⊥BA.
又∵PD⊥AE,且BA∩AE=A,
∴PD⊥平面BAE
∵BE?平面BAE
∴PD⊥BE,即BE⊥PD.
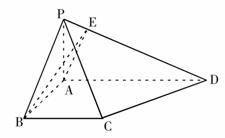
(Ⅱ)解:如图建立空间直角坐标系,
∵底面ABCD为直角梯形,∠BAD=90°,AD∥BC
∴CB⊥AB,
∵PA⊥底面ABCD,CB?底面ABCD
∴CB⊥PA,
∵PA∩AB=A
∴CB⊥平面PAB.
∴ 是平面PAB的法向量,且
是平面PAB的法向量,且 =(0,a,0).
=(0,a,0).
设平面PCD的一个法向量为 ,则
,则 .
.
而 =(-a,a,0),
=(-a,a,0),
∴由 =0.
=0.
得
∴
令y=1,∴
设向量 与
与 所成角为θ,
所成角为θ,
则cosθ= .
.
∴平面PAB与平面PCD所成锐二面角的余弦值为 .
.
点评:本题重点考查线面垂直的判定与性质,考查面面角,解题的关键是熟练掌握线面垂直的判定与性质,掌握平面法向量的求解方法.
(Ⅱ)利用空间向量,构建空间直角坐标系,分别求出平面PAB与平面PCD的法向量,从而可求平面PAB与平面PCD所成锐二面角的余弦值.
解答:
 (Ⅰ)证明:∵∠BAD=90°,∴BA⊥AD
(Ⅰ)证明:∵∠BAD=90°,∴BA⊥AD∵PA⊥底面ABCD,BA?底面ABCD
∴BA⊥PA.
∵PA∩AD=A,
∴BA⊥平面PAD.
∵PD?平面PAD.
∴PD⊥BA.
又∵PD⊥AE,且BA∩AE=A,
∴PD⊥平面BAE
∵BE?平面BAE
∴PD⊥BE,即BE⊥PD.
(Ⅱ)解:如图建立空间直角坐标系,
∵底面ABCD为直角梯形,∠BAD=90°,AD∥BC
∴CB⊥AB,
∵PA⊥底面ABCD,CB?底面ABCD
∴CB⊥PA,
∵PA∩AB=A
∴CB⊥平面PAB.
∴
 是平面PAB的法向量,且
是平面PAB的法向量,且 =(0,a,0).
=(0,a,0).设平面PCD的一个法向量为
 ,则
,则 .
.而
 =(-a,a,0),
=(-a,a,0),∴由
 =0.
=0.得

∴

令y=1,∴

设向量
 与
与 所成角为θ,
所成角为θ,则cosθ=
 .
.∴平面PAB与平面PCD所成锐二面角的余弦值为
 .
.点评:本题重点考查线面垂直的判定与性质,考查面面角,解题的关键是熟练掌握线面垂直的判定与性质,掌握平面法向量的求解方法.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
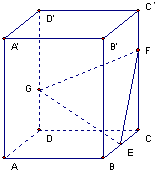 如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求:
如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求: 如图,在四棱柱P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=
如图,在四棱柱P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=