题目内容
已知向量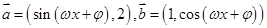 ,
,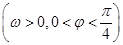 ,函数
,函数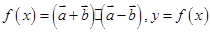 图象的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点
图象的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点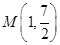 。
。
(1)求函数 的解析式
的解析式
(2)当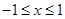 时,求函数
时,求函数 的单调区间。
的单调区间。
【答案】
(1)
(2)函数 的单调递减区间是
的单调递减区间是 ,单调递增区间是
,单调递增区间是
【解析】
试题分析:(1)
 ,由题意得周期
,由题意得周期 故
故 ,又图象过点
,又图象过点 所以
所以 ,即
,即 ,而
,而 ,故
,故 ,
,
则:
(2)当 时,
时,
 当
当 时,即
时,即 时,
时, 是减函数。
是减函数。
当 时,即
时,即 时,
时, 是增函数。
是增函数。
则函数 的单调递减区间是
的单调递减区间是 ,单调递增区间是
,单调递增区间是
考点:本题主要考查平面向量的坐标运算,和差倍半的三角函数,三角函数的图象和性质。
点评:典型题,属于常见题型,通过计算平面向量的数量积,得到三角函数式,灵活运用三角公式“化一”,进一步研究三角函数的性质。本题(II)涉及角的较小范围,易于出错。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
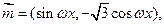
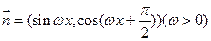 ,若函数
,若函数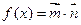 的最小正周期为
的最小正周期为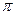
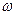 的值
的值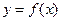 的图象向右平移
的图象向右平移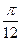 个单位,再将所得到的图象上各点的横坐标伸长到原来的
个单位,再将所得到的图象上各点的横坐标伸长到原来的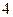 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数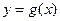 的图象,求
的图象,求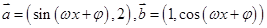 ,
,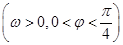 ,函数
,函数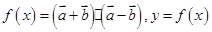 图象的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点
图象的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点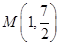 。
。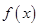 的解析式
的解析式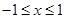 时,求函数
时,求函数 ,
, ,函数
,函数 .
.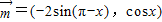 ,
,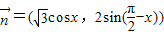 ,函数
,函数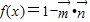 .
.