题目内容
已知向量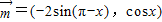 ,
,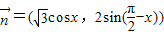 ,函数
,函数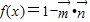 .
.(1)求函数f(x)的解析式;
(2)当x∈[0,π]时,求f(x)的单调递增区间;
(3)说明f(x)的图象可以由g(x)=sinx的图象经过怎样的变换而得到.
【答案】分析:(1)直接利用向量的数量积,通过二倍角公式与两角差的正弦函数,化简函数我一个角的一个三角函数的形式,即可求函数f(x)的解析式;
(2)利用正弦函数的单调增区间求出函数的单调增区间与x∈[0,π]取交集,即可求f(x)的单调递增区间;
法二通过x的范围,求出2x- 的范围,然后利用函数的最值时的2x-
的范围,然后利用函数的最值时的2x- 的值,即可得到单调增区间.
的值,即可得到单调增区间.
(3)利用左加右减,与伸缩变换的原则,直接说明f(x)的图象可以由g(x)=sinx的图象经过变换而得到.
解答:解:(1)∵ =
=
= 2分
2分
∴f(x)=1- =
= ,…(3分)
,…(3分)
∴f(x)= .…(4分)
.…(4分)
(2)由 ,
,
解得 ,…(6分)
,…(6分)
∵取k=0和1且x∈[0,π],得 和
和 ,
,
∴f(x)的单调递增区间为 和
和 .…(8分)
.…(8分)
法二:∵x∈[0,π],∴ ,
,
∴由 和
和 ,…(6分)
,…(6分)
解得 和
和 ,
,
∴f(x)的单调递增区间为 和
和 .…(8分)
.…(8分)
(3)g(x)=sinx的图象可以经过下面三步变换得到f(x)= 的图象:g(x)=sinx的图象向右平移
的图象:g(x)=sinx的图象向右平移 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变),最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),得到f(x)=
倍(纵坐标不变),最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),得到f(x)= 的图象.…(14分)(每一步变换2分)
的图象.…(14分)(每一步变换2分)
点评:本题借助向量的数量积的化简,求解函数的解析式,考查三角函数的基本性质,函数的图象的变换.
(2)利用正弦函数的单调增区间求出函数的单调增区间与x∈[0,π]取交集,即可求f(x)的单调递增区间;
法二通过x的范围,求出2x-
 的范围,然后利用函数的最值时的2x-
的范围,然后利用函数的最值时的2x- 的值,即可得到单调增区间.
的值,即可得到单调增区间.(3)利用左加右减,与伸缩变换的原则,直接说明f(x)的图象可以由g(x)=sinx的图象经过变换而得到.
解答:解:(1)∵
 =
=
=
 2分
2分∴f(x)=1-
 =
= ,…(3分)
,…(3分)∴f(x)=
 .…(4分)
.…(4分)(2)由
 ,
,解得
 ,…(6分)
,…(6分)∵取k=0和1且x∈[0,π],得
 和
和 ,
,∴f(x)的单调递增区间为
 和
和 .…(8分)
.…(8分)法二:∵x∈[0,π],∴
 ,
,∴由
 和
和 ,…(6分)
,…(6分)解得
 和
和 ,
,∴f(x)的单调递增区间为
 和
和 .…(8分)
.…(8分)(3)g(x)=sinx的图象可以经过下面三步变换得到f(x)=
 的图象:g(x)=sinx的图象向右平移
的图象:g(x)=sinx的图象向右平移 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变),最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),得到f(x)=
倍(纵坐标不变),最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),得到f(x)= 的图象.…(14分)(每一步变换2分)
的图象.…(14分)(每一步变换2分)点评:本题借助向量的数量积的化简,求解函数的解析式,考查三角函数的基本性质,函数的图象的变换.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
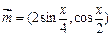 ,
, ,函数
,函数
 的最小正周期;
的最小正周期;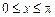 ,求
,求










 ,
, ,函数
,函数 .
. ,
, ,函数
,函数 .
. 在
在 上有解,求
上有解,求 的取值范围;
的取值范围; 中,
中, 分别是A,B,C所对的边,当(Ⅰ)中的
分别是A,B,C所对的边,当(Ⅰ)中的 时,求
时,求 的最小值.
的最小值. ,
, ,函数
,函数 .
. 的最小正周期以及单调递增区间;
的最小正周期以及单调递增区间; 时, 求
时, 求 在
在 内的所有实数根之和.
内的所有实数根之和.