题目内容
 A,B,C是圆O上的三点,∠AOB=120°,CO的延长线与线段AB交于点D,若
A,B,C是圆O上的三点,∠AOB=120°,CO的延长线与线段AB交于点D,若| OC |
| OA |
| OB |
[-2,-1]
[-2,-1]
.分析:利用已知条件,两边平方,结合基本不等式,即可求得结论.
解答:解:设圆的半径为1,则由题意m≤0,n≤0
∵
=m
+n
,|OC|=|OB|=|OA|=1,∠AOB=120°,
∴
2=m2+n2+2mn•
•
=m2+n2+2mn•cos120°=(m+n)2-3mn=1.
∴(m+n)2=1+3mn≥1,
∴m+n≤-1,
∵(m+n)2=1+3mn≤1+
(m+n)2,
∴(m+n)2≤4
∴m+n≥-2
∴m+n的取值范围是[-2,-1]
故答案为:[-2,-1]
∵
| OC |
| OA |
| OB |
∴
| OC |
| OA |
| OB |
∴(m+n)2=1+3mn≥1,
∴m+n≤-1,
∵(m+n)2=1+3mn≤1+
| 3 |
| 4 |
∴(m+n)2≤4
∴m+n≥-2
∴m+n的取值范围是[-2,-1]
故答案为:[-2,-1]
点评:本题考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
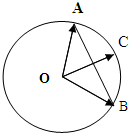 如图所示,点A,B,C是圆O上的三点,线段OC与线段AB交于圆内一点,若
如图所示,点A,B,C是圆O上的三点,线段OC与线段AB交于圆内一点,若| OC |
| OA |
| OB |
| A、0<m+n<1 |
| B、m+n>1 |
| C、m+n<-1 |
| D、-1<m+n<0 |
 如图,点A,B,C是圆O上的点,且AB=2,BC=
如图,点A,B,C是圆O上的点,且AB=2,BC= 如图,点A,B,C是圆O上的点,且AB=4,∠ACB=45°,则圆O的面积等于
如图,点A,B,C是圆O上的点,且AB=4,∠ACB=45°,则圆O的面积等于 (2012•杭州二模)如图所示,A,B,C是圆O上的三点,CO的延长线与线段BA的延长线交于圆O外的点D,若
(2012•杭州二模)如图所示,A,B,C是圆O上的三点,CO的延长线与线段BA的延长线交于圆O外的点D,若 A:(坐标系与参数方程选做题)在极坐标系中,由θ=0,θ=
A:(坐标系与参数方程选做题)在极坐标系中,由θ=0,θ=