题目内容
已知椭圆 :
: (
( )的右焦点为
)的右焦点为 ,且椭圆
,且椭圆 过点
过点 .
.
(1)求椭圆 的方程;
的方程;
(2)设斜率为 的直线
的直线 与椭圆
与椭圆 交于不同两点
交于不同两点 、
、 ,以线段
,以线段 为底边作等腰三角形
为底边作等腰三角形 ,其中顶点
,其中顶点 的坐标为
的坐标为 ,求△
,求△ 的面积.
的面积.
(1)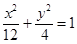 ;(2)
;(2)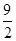 .
.
解析试题分析:(1)要确定椭圆方程,要确定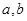 两个参数的值,因此需要两个条件,题中有焦点为
两个参数的值,因此需要两个条件,题中有焦点为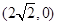 ,
,
即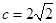 ,又椭圆过点
,又椭圆过点 ,代入方程又得到一个关于
,代入方程又得到一个关于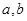 的等式,联立可解得
的等式,联立可解得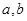 ;(2) 直线和圆锥曲线相交问题,一般都是设出直线方程,本题直线
;(2) 直线和圆锥曲线相交问题,一般都是设出直线方程,本题直线 的方程可设为
的方程可设为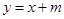 ,代入椭圆方程得到关于
,代入椭圆方程得到关于 的一元二次方程,再设交点为
的一元二次方程,再设交点为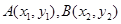 ,则可得
,则可得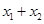 ,
,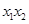 ,而条件等腰三角形
,而条件等腰三角形 的应用方法是底边
的应用方法是底边 边上的中线就是此边上的高,即取
边上的中线就是此边上的高,即取 中点为
中点为 ,则
,则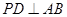 .由此可求得
.由此可求得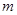 从而得到
从而得到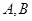 坐标,最终求得
坐标,最终求得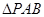 的面积.
的面积.
试题解析:(1)由已知得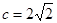 ,因为椭圆
,因为椭圆 过点
过点 ,所以
,所以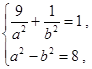 (2分)
(2分)
解得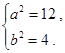 (5分)
(5分)
所以,椭圆 的方程为
的方程为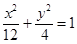 . (6分)
. (6分)
(2)设直线 的方程为
的方程为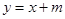 , (1分)
, (1分)
由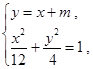 得
得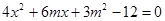 ① (2分)
① (2分)
因为直线 与椭圆
与椭圆 交于不同两点
交于不同两点 、
、 ,所以△
,所以△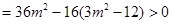 ,
,
所以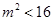 . (3分)
. (3分)
设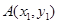 ,
,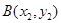 ,则
,则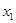 ,
,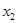 是方程①的两根,所以
是方程①的两根,所以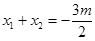 ,
,
设 的中点为
的中点为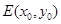 ,则
,则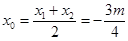 ,
,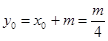 , (4分)
, (4分)
因为 是等腰三角形
是等腰三角形 的底边,所以
的底边,所以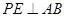 ,向量
,向量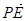 是直线
是直线 的一个法向量,
的一个法向量,
所以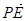 ∥向量
∥向量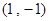 ,即
,即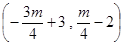 ∥向量
∥向量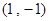 ,
,
所以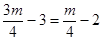 ,解得
,解得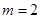 . (5分)
. (5分)
此时方程①变为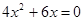 ,解得
,解得 ,
,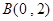 ,所以
,所以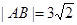 .
.
又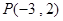 到直线
到直线
练习册系列答案
相关题目
 的离心率为
的离心率为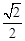 ,短轴端点分别为
,短轴端点分别为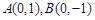 .
. ,
, 是椭圆
是椭圆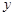 轴对称的两个不同点,直线
轴对称的两个不同点,直线 与
与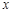 轴交于点
轴交于点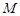 ,判断以线段
,判断以线段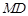 为直径的圆是否过点
为直径的圆是否过点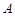 ,并说明理由.
,并说明理由.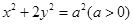 的一个顶点和两个焦点构成的三角形的面积为4.
的一个顶点和两个焦点构成的三角形的面积为4.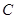 的方程;
的方程; 与椭圆
与椭圆 、
、 两点,试问,是否存在
两点,试问,是否存在 轴上的点
轴上的点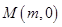 ,使得对任意的
,使得对任意的 ,
, 为定值,若存在,求出
为定值,若存在,求出 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.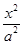 +
+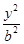 =1
=1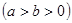 的离心率为
的离心率为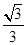 ,左焦点为F(-1,0),
,左焦点为F(-1,0),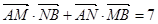 ,求直线L的方程;
,求直线L的方程;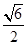 ?
? 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、 ,且
,且 (
( 为定值),线段
为定值),线段 的中点为
的中点为 ,与直线
,与直线 平行的切线的切点为
平行的切线的切点为 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
 、
、 表示出
表示出 垂直于
垂直于 轴;
轴; 的面积,证明
的面积,证明 、
、 ,再作与
,再作与 、
、 ,小张马上写出了
,小张马上写出了 、
、 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.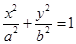 (a>b>0)的离心率为
(a>b>0)的离心率为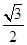 ,过其右焦点F与长轴垂直的弦长为1,
,过其右焦点F与长轴垂直的弦长为1, 的中心为原点
的中心为原点 ,长轴在
,长轴在 轴上,离心率
轴上,离心率 ,又椭圆
,又椭圆 .
.
 轴的直线
轴的直线 与椭圆
与椭圆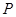 、
、 ,过
,过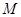 的圆,使椭圆
的圆,使椭圆 的面积
的面积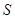 的最大值.
的最大值.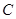 的离心率
的离心率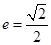 ,长轴的左右端点分别为
,长轴的左右端点分别为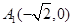 ,
,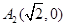 .
.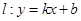 与曲线
与曲线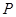 ,且与直线
,且与直线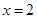 相交于点
相交于点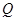 .
.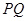 为直径的圆过定点
为直径的圆过定点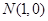 .
.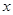 轴上的椭圆
轴上的椭圆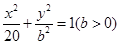 经过点
经过点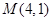 ,直线
,直线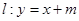
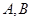 不同的两点.
不同的两点.
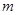 的取值范围;
的取值范围;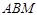 是以
是以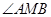 为直角的直角三角形,若存在,求出
为直角的直角三角形,若存在,求出