题目内容
数列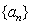 的前
的前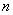 项和为
项和为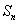 ,且满足
,且满足 ,
,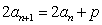 (
( 为常数,
为常数, ).
).
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)若数列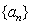 是等比数列,求实数
是等比数列,求实数 的值.
的值.
(Ⅲ)是否存在实数 ,使得数列
,使得数列 满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的
满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的 的值;若不存在,说明理由.
的值;若不存在,说明理由.
解:(Ⅰ)因为  ,
,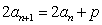 ,
,
所以 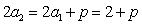 ,
,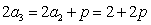 .
.
因为  ,
,
所以 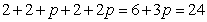 ,即
,即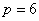 .
.
所以 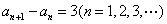 .
.
所以 数列 是以1为首项,3为公差的等差数列.
是以1为首项,3为公差的等差数列.
所以 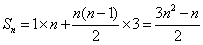 .
.
(Ⅱ)若数列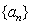 是等比数列,则
是等比数列,则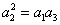 .
.
由(Ⅰ)可得: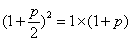 .
.
解得: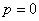 .
.
当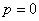 时,由
时,由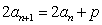 得:
得: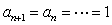 .
.
显然,数列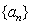 是以1为首项,1为公比的等比数列.
是以1为首项,1为公比的等比数列.
所以 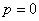 .
.
(Ⅲ)当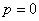 时,由(Ⅱ)知:
时,由(Ⅱ)知: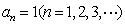 .
.
所以  ,即数列
,即数列 就是一个无穷等差数列.
就是一个无穷等差数列.
所以 当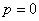 时,可以得到满足题意的等差数列.
时,可以得到满足题意的等差数列.
当 时,因为
时,因为  ,
,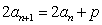 ,即
,即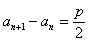 ,
,
所以 数列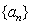 是以1为首项,
是以1为首项,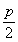 为公差的等差数列.
为公差的等差数列.
所以 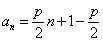 .
.
下面用反证法证明:当 时,数列
时,数列 中不能取出无限多项并按原来次序排列而成等差数列.
中不能取出无限多项并按原来次序排列而成等差数列.
假设存在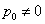 ,从数列
,从数列 中可以取得满足题意的无穷等差数列,不妨记为
中可以取得满足题意的无穷等差数列,不妨记为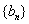 . 设数列
. 设数列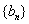 的公差为
的公差为 .
.
①当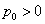 时,
时,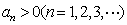 .
.
所以 数列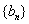 是各项均为正数的递减数列.
是各项均为正数的递减数列.
所以 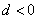 .
.
因为 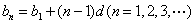 ,
,
所以 当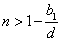 时,
时,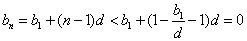 ,这与
,这与 矛盾.
矛盾.
②当 时,令
时,令 ,解得:
,解得: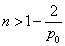 .
.
所以 当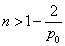 时,
时,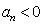 恒成立.
恒成立.
所以 数列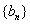 必然是各项均为负数的递增数列.
必然是各项均为负数的递增数列.
所以 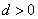 .
.
因为 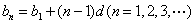 ,
,
所以 当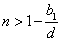 时,
时, ,这与
,这与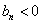 矛盾.
矛盾.
综上所述,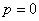 是唯一满足条件的
是唯一满足条件的 的值.
的值.

练习册系列答案
相关题目
 ⊥平面
⊥平面 ,直线m
,直线m 平面
平面 ,有
,有 下面
下面 四个命题:其中正确命题序号是
四个命题:其中正确命题序号是 

 中,点
中,点 为底面
为底面 上的动点. 若三棱锥
上的动点. 若三棱锥 的表面积最大,则
的表面积最大,则 处
处 的中点处
的中点处 的中点处
的中点处 处
处 的部分图象如图所示.
的部分图象如图所示. 及图中
及图中 的值;
的值; 在区间
在区间 上的最大值和最小值.
上的最大值和最小值. 假设至少有一个钝角
假设至少有一个钝角  假设至少有两个钝角
假设至少有两个钝角 假设没有一个钝角
假设没有一个钝角  假设没有一个钝角或假设至少有两个钝角
假设没有一个钝角或假设至少有两个钝角 的平均数是1006,则
的平均数是1006,则 的平均数是 .
的平均数是 . 若实数x,y满足约束条件
若实数x,y满足约束条件 则
则 的最大值是
的最大值是 B.
B. C.
C. D.
D.