题目内容

已知ABCD为平行四边形，则“|
AB
+
AD
|=|
AB
-
AD
|”是“ABCD为矩形”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
分析：方法一：|
AB
+
AD
|=|
AB
-
AD
|，两边平方，得到
AB
•
AD
=0?AB⊥AD，进而判断是矩形；
方法二：由|
AB
+
AD
|=|
AB
-
AD
|，知两对角线相等，故为矩形．
解答：解：∵|
AB
+
AD
|=|
AB
-
AD
|?|
AB
+
AD
|2=|
AB
-
AD
|2?2
AB
•
AD
=-2
AB
•
AD
?
AB
•
AD
=0?AB⊥AD，又ABCD为平行四边形，∴ABCD为矩形，
∴选C．
法二：|
AB
+
AD
|=|
AB
-
AD
|?|
AC
|=|
BD
|，对角线相等的平行四边形为矩形．
故选C．
点评：本题考查了向量的运算及几何意义，是基础题．
练习册系列答案
相关题目
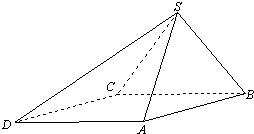精英家教网四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD，已知∠ABC=45°，AB=2，BC=2
2
，SA=SB=
3
．
（Ⅰ）证明：SA⊥BC；
（Ⅱ）求直线SD与平面SBC所成角的大小．
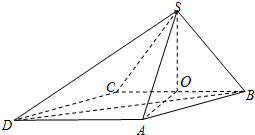精英家教网四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD．已知∠ABC=45°，AB=2，BC=2
2
，SA=SB=
3
．
（1）证明：SA⊥BC；
（2）求直线SD与平面SAB所成角的大小；
（3）求二面角D-SA-B的大小．
如图，已知四棱锥P-ABCD．
（1）若底面ABCD为菱形，∠DAB=60°，PA=PD，求证：PB⊥AD；
（2）若底面ABCD为平行四边形，E为PC的中点，在DE上取点F，过AP和点F的平面与平面BDE的交线为FG，求证：AP∥FG．
四棱锥S-ABCD中，底面ABCD为平行四边形，SO⊥底面ABCD，O在CB上．已知∠ABC=45°，AB=2，BC=2
2
，SA=SB=
3
，
（Ⅰ）求证：平面SCB⊥平面ABCD；
（Ⅱ）求四棱锥S-ABCD的体积；
（Ⅲ）求直线SD与平面SAB所成角的正弦值．
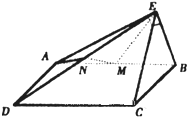精英家教网已知四边形ABCD为平行四边形，BC⊥平面ABE，AE⊥BE，BE=BC=1，AE=
3
，M为线段AB的中点，N为线段DE的中点，P为线段AE的中点．
（1）求证：MN⊥EA；
（2）求四棱锥M-ADNP的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网