题目内容
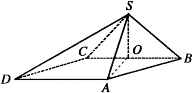
 四棱锥S-ABCD中,底面ABCD为平行四边形,SO⊥底面ABCD,O在CB上.已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,SO⊥底面ABCD,O在CB上.已知∠ABC=45°,AB=2,BC=2| 2 |
| 3 |
(Ⅰ)求证:平面SCB⊥平面ABCD;
(Ⅱ)求四棱锥S-ABCD的体积;
(Ⅲ)求直线SD与平面SAB所成角的正弦值.
分析:(I)利用SO⊥底面ABCD,可证平面SCB⊥平面ABCD;
(II)利用余弦定理求得cos∠SBA,再利用三面角余弦公式求得cos∠SBA,从而求得OB,SO的长,然后利用棱锥的体积公式计算.
(III)先证明OA⊥OB,再以O点位原点建立空间直角坐标系,求得平面SAB的法向量,利用向量坐标运算求线面角的正弦.
(II)利用余弦定理求得cos∠SBA,再利用三面角余弦公式求得cos∠SBA,从而求得OB,SO的长,然后利用棱锥的体积公式计算.
(III)先证明OA⊥OB,再以O点位原点建立空间直角坐标系,求得平面SAB的法向量,利用向量坐标运算求线面角的正弦.
解答:解:( I)∵SO?平面SBC,SO⊥底面ABCD,
∴平面SCB⊥平面ABCD.
(II)∵AB=2,SA=SB=
,∴cos∠SBA=
=
,
由三面角余弦公式得:cos∠SBA=cos∠SBO•cos∠ABC,即
=cos∠SBO•cos450⇒cos∠SBO=
又cos∠SBO=
,
∴OB=SBcos∠SBO=
×
=
又∵BC=2
,
∴O为BC的中点,SO=
=1,
∴VS-ABCD=
SABCD×SO=
×BC×AB×sin45°×SO=
×2
×2×
×1=
,
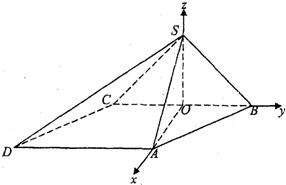
( III)如图,以O为原点,OA为x轴,OB为y轴,OS为z轴,建立空间直角坐标系O-xyz,
则A(
,0,0),B(0,
,0),C(0,-
,0),D(
,-2
,0),S(0,0,1)
则
=(
,0,-1),
=(-
,
,0)
设
=(x,y,z)为平面SAB的一个法向量,
由
可得:
即
取x=l,得
=(1,1,
)
而
=(
,-2
,-1),
设直线,SD与平面SAB所成的角为θ,
则sinθ=
=
故直线SD与平面SAB所成角的正弦值为
∴平面SCB⊥平面ABCD.
(II)∵AB=2,SA=SB=
| 3 |
| 4+3-3 | ||
2×2×
|
| ||
| 3 |
由三面角余弦公式得:cos∠SBA=cos∠SBO•cos∠ABC,即
| ||
| 3 |
| ||
| 3 |
又cos∠SBO=
| OB |
| SB |
∴OB=SBcos∠SBO=
| 3 |
| ||
| 3 |
| 2 |

又∵BC=2
| 2 |
∴O为BC的中点,SO=
| SB2-OB2 |
∴VS-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| ||
| 2 |
| 4 |
| 3 |
( III)如图,以O为原点,OA为x轴,OB为y轴,OS为z轴,建立空间直角坐标系O-xyz,
则A(
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
则
| SA |
| 2 |
| AB |
| 2 |
| 2 |

设
| n |
由
|
|
即
|
取x=l,得
| n |
| 2 |
而
| SD |
| 2 |
| 2 |
设直线,SD与平面SAB所成的角为θ,
则sinθ=
|
| ||||
|
|
| ||
| 11 |
故直线SD与平面SAB所成角的正弦值为
| ||
| 11 |
点评:本题考查了面面垂直的证明.考查了棱锥的体积计算,考查了利用向量坐标运算求线面角的正弦值,考查学生的空间想象能力,运算能力,综合性强.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
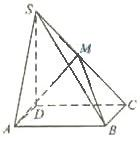 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=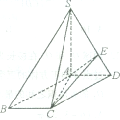 如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥平面ABCD,AB=2,AD=1,
如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥平面ABCD,AB=2,AD=1,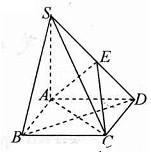 如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,SB=SD=2
如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,SB=SD=2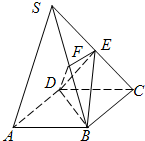 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,SD=AD,DF⊥SB垂足为F,E是SD的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,SD=AD,DF⊥SB垂足为F,E是SD的中点.