题目内容
已知椭圆
上的点
到左右两焦点
的距离之和为
，离心率为
.
（Ⅰ）求椭圆的方程；
（Ⅱ）过右焦点
的直线
交椭圆于
两点，若
轴上一点
满足
，求直线的斜率
的值.
解：（Ⅰ）
，∴
，∴
，
∴
椭圆的标准方程为
（Ⅱ）已知
,设直线的方程为
，
联立直线与椭圆的方程
，化简得：
∴
，
∴
的中点坐标为
①当
时，的中垂线方程为
∵，∴点
在的中垂线上，将点的坐标代入直线方程得：
，即
解得
或
②当
时，的中垂线方程为
，满足题意.
∴斜率的取值为
.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
＝
，
＝
，则
＝___ ____．(用
的定义域为
，数列
是公差为
的等差数列，且
，记
．
，下列说法正确的是（ ）
时，
时，
的渐近线与圆
相切，则
( )
B. 2 C. 3 D. 6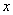
轴，且过点
，则抛物线的方程为 _____
是
的（ ）
和直线
，抛物线
上一动点
到直线
和直线
的距离之和的最小值是( )
D.
，则 ( )
是经过椭圆
＝1的中心且相互垂直的两条直线, 分别交椭圆于
, 则四边形
的面积的最小值是（ ）
