题目内容
2.已知函数f(x)=$\frac{1}{x+1}$(x∈(2,3]).(1)求证:函数是减函数;
(2)求函数的最值.
分析 (1)运用单调性的定义证明,注意作差、变形和定符号、下结论几个步骤;
(2)运用函数f(x)为(2,3]上的减函数,即可得到所求最值.
解答 解:(1)证明:设2<m<n≤3,即有f(m)-f(n)=$\frac{1}{1+m}$-$\frac{1}{1+n}$
=$\frac{n-m}{(1+m)(1+n)}$,
由2<m<n≤3,可得n-m>0,(1+m)(1+n)>0,
则f(m)>f(n),则函数f(x)为(2,3]上的减函数;
(2)由函数f(x)为(2,3]上的减函数,
可得f(3)为最小值,且为$\frac{1}{4}$,无最大值.
点评 本题考查函数的带动下的证明,注意运用定义法,考查函数的最值的求法,运用函数的单调性,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
11.已知$\frac{π}{2}$≤β<α<$\frac{3π}{4}$,sin(α+β)=-$\frac{3}{5}$,cos(α-β)=$\frac{12}{13}$,则cos2β的值为( )
| A. | -$\frac{63}{65}$ | B. | $\frac{63}{65}$ | C. | $\frac{33}{65}$ | D. | -$\frac{33}{65}$ |
5.已知一次函数f(x)的图象不过第四象限,且f(f(x))=4x+3,则f(x)的表达式为( )
| A. | 2x+1 | B. | -2x-3 | C. | -2x+1 | D. | 2x+3 |
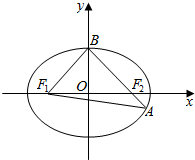 如图所示,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,左,右焦点分别为F1,F2上顶点为B,延长BF2交椭圆C于点A,且△ABF1的周长为8.
如图所示,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,左,右焦点分别为F1,F2上顶点为B,延长BF2交椭圆C于点A,且△ABF1的周长为8. 如图,在四陵锥P-ABCD中,AB∥CD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.求证:
如图,在四陵锥P-ABCD中,AB∥CD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.求证: