题目内容
在平面直角坐标系xOy中,已知圆M过坐标原点O且圆心在曲线y=
上.
(Ⅰ)若圆M分别与x轴、y轴交于点A、B(不同于原点O),求证:△AOB的面积为定值;
(Ⅱ)设直线l:y=-
x+4与圆M 交于不同的两点C,D,且|OC|=|OD|,求圆M的方程;
(Ⅲ)设直线y=
与(Ⅱ)中所求圆M交于点E、F,P为直线x=5上的动点,直线PE,PF与圆M的另一个交点分别为G,H,求证:直线GH过定点.
| ||
| x |
(Ⅰ)若圆M分别与x轴、y轴交于点A、B(不同于原点O),求证:△AOB的面积为定值;
(Ⅱ)设直线l:y=-
| ||
| 3 |
(Ⅲ)设直线y=
| 3 |
考点:圆的标准方程,直线与圆的位置关系
专题:计算题,直线与圆
分析:(Ⅰ)由题意可设圆M的方程为(x-t)2+(y-
)2=t2+
,求出圆M分别与x轴、y轴交于点A、B的坐标,利用面积公式,可得:△AOB的面积为定值;
(Ⅱ)由|OC|=|OD|,知OM⊥l,解得t=±1,再验证,即可求圆M的方程;
(Ⅲ)设P(5,y0),G(x1,y1),H(x2,y2),整理得2x1x2-7(x1+x2)+20=0.①设直线GH的方程为y=kx+b,代入(x-1)2+(y-
)2=4,利用韦达定理,确定直线方程,即可得出结论.
| ||
| t |
| 3 |
| t2 |
(Ⅱ)由|OC|=|OD|,知OM⊥l,解得t=±1,再验证,即可求圆M的方程;
(Ⅲ)设P(5,y0),G(x1,y1),H(x2,y2),整理得2x1x2-7(x1+x2)+20=0.①设直线GH的方程为y=kx+b,代入(x-1)2+(y-
| 3 |
解答:
解:(Ⅰ)由题意可设圆M的方程为(x-t)2+(y-
)2=t2+
,
即x2+y2-2tx-
y=0.
令x=0,得y=
;令y=0,得x=2t.
∴S△AOB=
|OA|•|OB|=
|2t|•|
|=2
(定值).…(4分)
(Ⅱ)由|OC|=|OD|,知OM⊥l.
所以kOM=
=
,解得t=±1.
当t=1时,圆心M(1,
)到直线l:y=-
x+4的距离d=2(
-1)小于半径,符合题意;
当t=-1时,圆心M(-1,-
)到直线l:y=-
x+4的距离d=2(
+1)大于半径,不符合题意.
所以,所求圆M的方程为(x-1)2+(y-
)2=4.…(8分)
(Ⅲ)设P(5,y0),G(x1,y1),H(x2,y2),又知E(-1,
),F(3,
),
所以kPE=
=
=kGE,kPF=
=
=kFH.
因为3kPE=kPF,所以9×
=
.
将(y1-
)2=4-(x1-1)2,(y2-
)2=4-(x2-1)2代入上式,
整理得2x1x2-7(x1+x2)+20=0.①
设直线GH的方程为y=kx+b,代入(x-1)2+(y-
)2=4,
整理得(1+k2)x2+(2kb-2
k-2)x+b2-2
b=0.
所以x1+x2=-
,x1•x2=
.
代入①式,并整理得b2+(7k-2
)b+10k2-7
b+3=0,
即(b+2k-
)(b+5k-
)=0,
解得b=
-2k或b=
-5k.
当b=
-2k时,直线GH的方程为y=k(x-2)+
,过定点(2,
);
当b=
-5k时,直线GH的方程为y=k(x-5)+
,过定点(5,
)…(14分)
| ||
| t |
| 3 |
| t2 |
即x2+y2-2tx-
2
| ||
| t |
令x=0,得y=
2
| ||
| t |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| t |
| 3 |
(Ⅱ)由|OC|=|OD|,知OM⊥l.
所以kOM=
| ||
| t2 |
| 3 |
当t=1时,圆心M(1,
| 3 |
| ||
| 3 |
| 3 |
当t=-1时,圆心M(-1,-
| 3 |
| ||
| 3 |
| 3 |
所以,所求圆M的方程为(x-1)2+(y-
| 3 |
(Ⅲ)设P(5,y0),G(x1,y1),H(x2,y2),又知E(-1,
| 3 |
| 3 |
所以kPE=
y0-
| ||
| 6 |
y1-
| ||
| x1+1 |
y0-
| ||
| 2 |
y2-
| ||
| x2-3 |
因为3kPE=kPF,所以9×
(y1-
| ||
| (x1+1)2 |
(y2-
| ||
| (x2-3)2 |
将(y1-
| 3 |
| 3 |
整理得2x1x2-7(x1+x2)+20=0.①
设直线GH的方程为y=kx+b,代入(x-1)2+(y-
| 3 |
整理得(1+k2)x2+(2kb-2
| 3 |
| 3 |
所以x1+x2=-
2kb-2
| ||
| 1+k2 |
b2-2
| ||
| 1+k2 |
代入①式,并整理得b2+(7k-2
| 3 |
| 3 |
即(b+2k-
| 3 |
| 3 |
解得b=
| 3 |
| 3 |
当b=
| 3 |
| 3 |
| 3 |
当b=
| 3 |
| 3 |
| 3 |
点评:本题考查圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知函数f(x)=
sin2x+cos2x,若f(x-φ)为偶函数,则φ的一个值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=
,则f[f(4)]=( )
|
| A、2 | B、4 | C、8 | D、16 |
与函数y=x相等的函数是( )
A、y=(
| |||
B、y=
| |||
C、y=
| |||
D、y=
|
如图所示程序框图中,某班50名学生,在一次数学考试中,an表示学号为n的学生的成绩,则( )
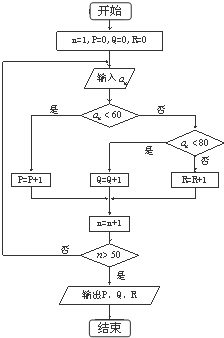

| A、P表示成绩不高于60分的人数 |
| B、Q表示成绩低于80分的人数 |
| C、R表示成绩高于80分的人数 |
| D、Q表示成绩不低于60分,且低于80分人数 |