题目内容
已知 =(1+cosα,sinα),
=(1+cosα,sinα), =(1-cosβ,sinβ),
=(1-cosβ,sinβ), ,α∈(0,π),β∈(π,2π),向量
,α∈(0,π),β∈(π,2π),向量 与
与 夹角为θ1,向量
夹角为θ1,向量 与
与 夹角为θ2,且θ1-θ2=
夹角为θ2,且θ1-θ2=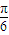 ,若△ABC中角A、B、C的对边分别为a、b、c,且角A=β-α.
,若△ABC中角A、B、C的对边分别为a、b、c,且角A=β-α.求(Ⅰ)求角A 的大小;
(Ⅱ)若△ABC的外接圆半径为
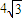 ,试求b+c取值范围.
,试求b+c取值范围.
【答案】分析:(Ⅰ)先根据条件求出 以及
以及 ,再结合θ1、θ2为向量夹角即可求出
,再结合θ1、θ2为向量夹角即可求出 ,进而求出角A 的大小;
,进而求出角A 的大小;
(Ⅱ)先根据正弦定理得到 ,再结合
,再结合 ,即可求出结论.
,即可求出结论.
解答:解:(Ⅰ)据题设,并注意到α、β的范围, ----------------------(2分)
----------------------(2分)
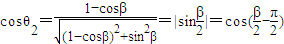 ,--------------------(4分)
,--------------------(4分)
由于θ1、θ2为向量夹角,故θ1、θ2∈[0,π],
而 ,
,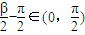 ,故有
,故有 ,得
,得 .--(7分)
.--(7分)
(Ⅱ)由正弦定理 ,-------(10分)
,-------(10分)
得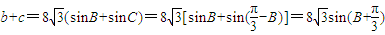 --------(12分)
--------(12分)
注意到 ,从而得
,从而得 .------------------------(14分)
.------------------------(14分)
点评:本题主要考查向量的数量积求向量的夹角以及正弦定理的应用.解决第二问的关键在于根据正弦定理得到 .
.
 以及
以及 ,再结合θ1、θ2为向量夹角即可求出
,再结合θ1、θ2为向量夹角即可求出 ,进而求出角A 的大小;
,进而求出角A 的大小;(Ⅱ)先根据正弦定理得到
 ,再结合
,再结合 ,即可求出结论.
,即可求出结论.解答:解:(Ⅰ)据题设,并注意到α、β的范围,
 ----------------------(2分)
----------------------(2分)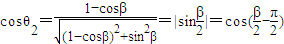 ,--------------------(4分)
,--------------------(4分)由于θ1、θ2为向量夹角,故θ1、θ2∈[0,π],
而
 ,
,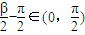 ,故有
,故有 ,得
,得 .--(7分)
.--(7分)(Ⅱ)由正弦定理
 ,-------(10分)
,-------(10分)得
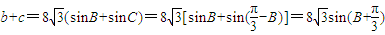 --------(12分)
--------(12分)注意到
 ,从而得
,从而得 .------------------------(14分)
.------------------------(14分)点评:本题主要考查向量的数量积求向量的夹角以及正弦定理的应用.解决第二问的关键在于根据正弦定理得到
 .
. 
练习册系列答案
相关题目
已知向量
=(1-cosθ,1),
=(
,1+sinθ),且
∥
,则锐角θ等于( )
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、75° |