题目内容
圆:x2+y2-2x-2y+1=0上的点到直线x-y=2的距离最小值是
- A.2
- B.

- C.

- D.
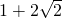
C
分析:把圆的方程化为标准方程,找出圆心坐标和圆的半径r,再利用点到直线的距离公式求出圆心到已知直线的距离d,用d-r即可求出所求的距离最小值.
解答:把圆的方程化为标准方程得:(x-1)2+(y-1)2=1,
∴圆心坐标为(1,1),半径r=1,
∴圆心到直线x-y=2的距离d=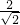 =
= ,
,
则圆上的点到已知直线距离最小值为d-r= -1.
-1.
故选C
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,其中根据题意得出圆心到已知直线的距离减去圆的半径为所求距离的最小值是解本题的关键.
分析:把圆的方程化为标准方程,找出圆心坐标和圆的半径r,再利用点到直线的距离公式求出圆心到已知直线的距离d,用d-r即可求出所求的距离最小值.
解答:把圆的方程化为标准方程得:(x-1)2+(y-1)2=1,
∴圆心坐标为(1,1),半径r=1,
∴圆心到直线x-y=2的距离d=
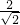 =
= ,
,则圆上的点到已知直线距离最小值为d-r=
 -1.
-1.故选C
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,其中根据题意得出圆心到已知直线的距离减去圆的半径为所求距离的最小值是解本题的关键.

练习册系列答案
相关题目
如果直线l将圆:x2+y2-2x-4y=0平分,且不通过第四象限,那么l的斜率的取值范围是( )
| A、[0,2] | ||
| B、[0,1] | ||
C、[0,
| ||
D、[0,
|