题目内容
（2012•青岛一模）已知从点（-2，1）发出的一束光线，经x轴反射后，反射光线恰好平分圆：x2+y2-2x-2y+1=0的圆周，则反射光线所在的直线方程为（ ）
分析：由题意可得反射光线所在的直线经过圆心M（1，1），点P（-2，1）关于x轴的对称点Q（-2，-1）在反射光线所在的直线上，用两点式求得反射光线所在的直线方程．
解答：解：由题意可得反射光线所在的直线经过圆：x2+y2-2x-2y+1=0的圆心M（1，1），
由反射定律可得点P（-2，1）关于x轴的对称点Q（-2，-1）在反射光线所在的直线上，
根据M、Q两点的坐标，用两点式求得反射光线所在的直线方程为
=
，
化简可得 2x-3y+1=0，
故选C．
由反射定律可得点P（-2，1）关于x轴的对称点Q（-2，-1）在反射光线所在的直线上，
根据M、Q两点的坐标，用两点式求得反射光线所在的直线方程为
| y+1 |
| 1+1 |
| x+2 |
| 1+2 |
化简可得 2x-3y+1=0，
故选C．
点评：本题主要考查用两点式求直线方程，判断反射光线所在的直线经过圆心M（1，1），是解题的突破口，属于中档题．
练习册系列答案
相关题目
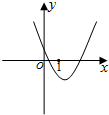（2012•青岛一模）已知a＞b，函数f（x）=（x-a）（x-b）的图象如图所示，则函数g（x）=loga（x+b）的图象可能为