题目内容
如图,△OBC的三个顶点坐标分别为(0,0)、(1,0)、(0,2),设P1为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n,Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn),an= yn+yn+1+yn+2.
yn+yn+1+yn+2.

(Ⅰ)求a1,a2,a3及an;
(Ⅱ)证明yn+4=1- ,n∈N*,
,n∈N*,
(Ⅲ)若记bn=y4n+4-y4n,n∈N*,证明{bn}是等比数列.
(Ⅰ)因为y1=y2=y4=1,y3= ,y5=
,y5= ,所以a1=a2=a3=2.又由题意可知yn+3=
,所以a1=a2=a3=2.又由题意可知yn+3= .
.
∴an+1= yn+1+yn+2+yn+3=
yn+1+yn+2+yn+3= yn+1+yn+2+
yn+1+yn+2+ =
= yn+yn+1+yn+2=an,∴{an}为常数列.∴an=a1=2,n∈N*.
yn+yn+1+yn+2=an,∴{an}为常数列.∴an=a1=2,n∈N*.
(Ⅱ)将等式 yn+yn+1+yn+2=2两边除以2,得
yn+yn+1+yn+2=2两边除以2,得 yn+
yn+ =1,又∵yn+4=
=1,又∵yn+4= ,∴yn+4=1-
,∴yn+4=1- .
.
(Ⅲ)∵bn+1=y4n+8-y4n+4= -
- =-
=- (y4n+4-y4n)=-
(y4n+4-y4n)=-  bn,又∵b1=y8-y4=-
bn,又∵b1=y8-y4=- ≠0,∴{bn}是公比为-
≠0,∴{bn}是公比为- 的等比数列.
的等比数列.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 恒在直线
恒在直线 上方,则实数
上方,则实数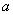 的取值范围为 .
的取值范围为 .  向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系x=2000
向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系x=2000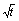 ,若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
,若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格). (元)表示为年产量t(吨)的函数,并求出乙方获得最大利润的年产量.
(元)表示为年产量t(吨)的函数,并求出乙方获得最大利润的年产量.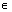 N.
N. 的右焦点为
的右焦点为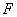 ,若过点
,若过点 且倾斜角为
且倾斜角为 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( ) B.
B. C.
C. D.
D.
 与曲线
与曲线 只有一个公共点,求实数
只有一个公共点,求实数 的取值集合是_______
的取值集合是_______