题目内容
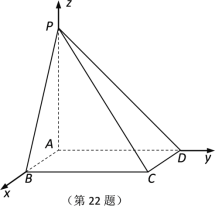
【题目】如图,在平面直角坐标系xOy中,![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,点P是椭圆E上一点,满足
的左,右焦点,点P是椭圆E上一点,满足![]() 轴,
轴,![]() .
.
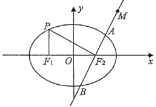
(1)求椭圆E的离心率;
(2)过点![]() 的直线l与椭圆E交于两点A,B,若在椭圆B上存在点Q,使得四边形OAQB为平行四边形,求直线l的斜率.
的直线l与椭圆E交于两点A,B,若在椭圆B上存在点Q,使得四边形OAQB为平行四边形,求直线l的斜率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据![]() ,
,![]() ,
,![]() ,建立
,建立![]() 的方程即可求解(2)斜率不存在时不符合题意,斜率存在时利用平行四边形的对角线互相平分,求出AB 中点,可得出Q坐标,利用点在椭圆上上求出斜率.
的方程即可求解(2)斜率不存在时不符合题意,斜率存在时利用平行四边形的对角线互相平分,求出AB 中点,可得出Q坐标,利用点在椭圆上上求出斜率.
(1)由![]() 轴,得
轴,得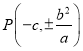 ,所以
,所以![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,
,
即![]() ,得
,得![]() ,
,
解得![]() 或
或![]() (舍),所以
(舍),所以![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
椭圆E方程可化为![]() .
.
若直线l斜率不存在,直线![]() ,与椭圆E只有一个交点,不成立.
,与椭圆E只有一个交点,不成立.
(法一)设直线l方程为![]() ,
,![]() ,
,![]() ,AB中点
,AB中点![]() ,
,
因为直线l过点![]() ,所以
,所以![]() ,
,
联立方程组![]() ,得
,得![]() .
.
![]() ,得
,得![]() .
.
由韦达定理,![]() ,
,![]() ,
,
得![]() ,
,![]() ,即点.
,即点.
因为平行四边形OAQB,所以点![]() ,
,
因为点Q在椭圆上,所以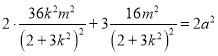 ,
,
化简得![]() .
.
由![]() ,得
,得![]() ,解得
,解得![]() .
.
(法二)设直线l的方程为![]() ,
,![]() ,
,![]() ,AB中点
,AB中点![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,得
,得![]() .
.
由韦达定理,![]() ,
,![]() ,
,
得![]() ,
,![]() ,即点
,即点![]() .
.
因为平行四边形OAQB,所以点![]() ,
,
因为点Q在椭圆上,所以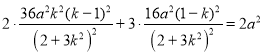 ,
,
化简得![]() ,解得
,解得![]() .
.

练习册系列答案
相关题目
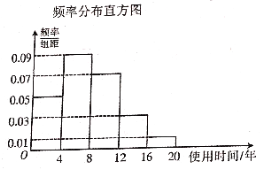
【题目】为了解一款电冰箱的使用时间和市民对这款电冰箱的购买意愿,研究人员对该款电冰箱进行了相应的抽样调查,得到数据的统计图表如下:
购买意愿市民年龄 | 不愿意购买该款电冰箱 | 愿意购买该款电冰箱 | 总计 |
40岁以上 | 600 | 800 | |
40岁以下 | 400 | ||
总计 | 800 |
(1)根据图中的数据,估计该款电冰箱使用时间的中位数;
(2)完善表中数据,并据此判断是否有![]() 的把握认为“愿意购买该款电冰箱“与“市民年龄”有关;
的把握认为“愿意购买该款电冰箱“与“市民年龄”有关;
(3)用频率估计概率,若在该电冰箱的生产线上随机抽取3台,记其中使用时间不低于4年的电冰箱的台数为![]() ,求
,求![]() 的期望.
的期望.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|