题目内容
已知数列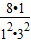 ,
,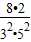 ,…,
,…,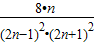 ,…,Sn为该数列的前n项和,
,…,Sn为该数列的前n项和,(1)计算S1,S2,S3,S4,
(2)根据计算结果,猜想Sn的表达式,并用数学归纳法进行证明.
【答案】分析:(1)按照数列和的定义计算即可
(2)按照数学归纳法的证明步骤进行证明.
解答:解:(1)S1=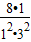 =
= ,
,
S2=
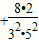 =
=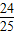 ,
,
S3=S2+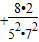 =
=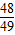 ,
,
S4=S3+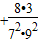 =
=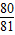 .
.
推测Sn=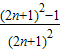 (n∈N*).用数学归纳法证明如下:…(5分)
(n∈N*).用数学归纳法证明如下:…(5分)
(1)当n=1时,S1=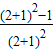 =
= ,等式成立
,等式成立
(2)假设当n=k时,等式成立,
即Sk=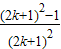 ,那么当n=k+1时,
,那么当n=k+1时,
Sk+1=Sk+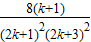
=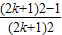 +
+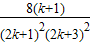
=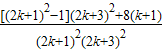
=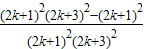
=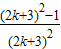
=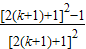
也就是说,当n=k+1时,等式成立.
根据(1)和(2),可知对一切n∈N*,等式均成立…(10分)
点评:本题主要考查数学归纳法的应用,用归纳法证明数学命题时的基本步骤:(1)检验n=1成立(2)假设n=k时成立,由n=k成立推导n=k+1成立,要注意由归纳假设到检验n=k+1的递推.
(2)按照数学归纳法的证明步骤进行证明.
解答:解:(1)S1=
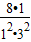 =
= ,
,S2=

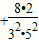 =
=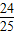 ,
,S3=S2+
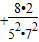 =
=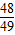 ,
,S4=S3+
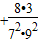 =
=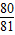 .
.推测Sn=
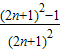 (n∈N*).用数学归纳法证明如下:…(5分)
(n∈N*).用数学归纳法证明如下:…(5分)(1)当n=1时,S1=
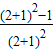 =
= ,等式成立
,等式成立(2)假设当n=k时,等式成立,
即Sk=
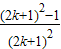 ,那么当n=k+1时,
,那么当n=k+1时,Sk+1=Sk+
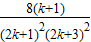
=
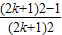 +
+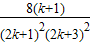
=
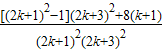
=
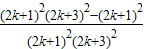
=
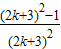
=
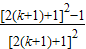
也就是说,当n=k+1时,等式成立.
根据(1)和(2),可知对一切n∈N*,等式均成立…(10分)
点评:本题主要考查数学归纳法的应用,用归纳法证明数学命题时的基本步骤:(1)检验n=1成立(2)假设n=k时成立,由n=k成立推导n=k+1成立,要注意由归纳假设到检验n=k+1的递推.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
已知数列an是首项为1的等比数列,Sn是an的前n项和,且S6=9S3,则数列an的通项公式是( )
| A、2n-1 | B、21-n | C、31-n | D、3n-1 |
已知数列
、
、
、
、3
…那么7
是这个数列的第几项( )
| 2 |
| 6 |
| 10 |
| 14 |
| 2 |
| 2 |
| A、23 | B、24 | C、19 | D、25 |