题目内容
解不等式:x2-3ax+(a+1)(2a-1)>0.
考点:一元二次不等式的解法
专题:计算题,分类讨论,不等式的解法及应用
分析:x2-3ax+(a+1)(2a-1)>0,即为(x-a-1)(x-2a+1)>0,讨论当a=2时,当a>2时,当a<2时,两根的大小,由二次不等式的解法即可得到解集.
解答:
解:x2-3ax+(a+1)(2a-1)>0,
即为(x-a-1)(x-2a+1)>0,
当a=2时,不等式即为(x-3)2>0,解得x≠3;
当a>2时,a+1<2a-1,解得,x>2a-1或x<a+1,
当a<2时,a+1>2a-1,解得,x<2a-1或x>a+1,
综上,当a=2时,解集为{x|x≠3,且x∈R};
当a>2时,解集为{x|x>2a-1或x<a+1};
当a<2时,解集为{x|x<2a-1或x>a+1}.
即为(x-a-1)(x-2a+1)>0,
当a=2时,不等式即为(x-3)2>0,解得x≠3;
当a>2时,a+1<2a-1,解得,x>2a-1或x<a+1,
当a<2时,a+1>2a-1,解得,x<2a-1或x>a+1,
综上,当a=2时,解集为{x|x≠3,且x∈R};
当a>2时,解集为{x|x>2a-1或x<a+1};
当a<2时,解集为{x|x<2a-1或x>a+1}.
点评:本题考查含参数二次不等式的解法,考查分类讨论的思想方法,考查运算能力,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
已知向量|
|=
,|
|=2,
与
的夹角为30°,则|
-
|的值( )
| AB |
| 3 |
| AC |
| AB |
| AC |
| AC |
| AB |
| A、1 | ||
| B、13 | ||
C、
| ||
D、2-
|
如果函数y=f(x)的图象经过点(0,1),那么函数y=f-1(x)+2的反函数的图象过点( )
| A、(3,0) |
| B、(0,3) |
| C、(1,2) |
| D、(2,1) |
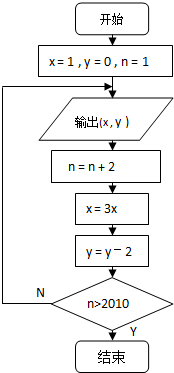 已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),…(xn,yn),…
已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),…(xn,yn),…