题目内容

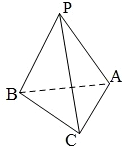
如图，在三棱锥P-ABC中，PA=PB=PC=BC，且∠BAC=
π
2
，则PA与底面ABC所成角为______．
∵PA=PB=PC，∴P在底面的射影E是△ABC的外心，又∠BAC=
π
2

故E是BC的中点，所以PA与底面ABC所成角为∠PAE，等边三角形PBC中，
PE=
3
2
，直角三角形ABC中，AE=
1
2
BC=
1
2
，又PA=1，
∴三角形PAE中，tan∠PAE=
PE
AE
=
3
∴∠PAE=
π
3
，
则PA与底面ABC所成角为
π
3
．
练习册系列答案
相关题目
如图，在正方体ABCD-A1B1C1D中，异面直线A1D与D1C所成的角为______度；直线A1D与平面AB1C1D所成的角为______度．
如图，在棱长为2的正方体ABCD-A1B1C1D1中，M，N分别是A1A，B1B的中点．
（1）求直线D1N与平面A1ABB1所成角的大小；
（2）求直线CM与D1N所成角的正弦值；
（3）（理科做）求点N到平面D1MB的距离．
将等边三角形ABC沿中线AD对折使BD⊥AC，那么AB与平面ACD所成的角是______．
在棱长都为a的正三棱柱ABC-A1B1C1中，P是A1B的中点．
（Ⅰ）求PC与平面ABB1A1所成的角；
（Ⅱ）求C1到平面PAC的距离．
如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5AA1=4，点D是AB的中点．
（1）求证：AC⊥BC1；
（2）求多面体ADC-A1B1C1的体积；
（3）求二面角D-CB1-B的平面角的正切值．
已知边长为
m
的正方形ABCj沿对角线AC折成直二面角，使j到P的位置．
（四）求直线PA与BC所成的角；
（m）若M为线段BC上的动点，当BM：BC为何值时，平面PAC与平面PAM所成的锐二面角为45°．
如图，在正三棱柱ABC-A1B1C1中，点D，D1分别为棱BC，B1C1的中点．
（1）求证：直线A1D1∥平面ADC1．
（2）求证：平面ADC1⊥平面BCC1B1；
（3）设底面边长为2，侧棱长为4，求二面角C1-AD-C的余弦值．
已知正方形ABCD沿其对角线AC将△ADC折起，设AD与平面ABC所成的角为β，当β取最大值时，二面角B-AC-D的大小为（　　）
A．120°B．90°C．60°D．45°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网