题目内容
若关于x的不等式(1+k2)x≤k4+4的解集是M,则对任意实常数k,总有( )A.2∈M,0∈M B.2![]() M,0
M,0![]() M
M
C.2∈M,0![]() M D.2
M D.2![]() M,0∈M
M,0∈M
解析:M={x|x≤![]() },
},
∵![]()
=k2-1+![]() =(k2+1)+
=(k2+1)+![]() -2
-2
≥![]() -2>2,
-2>2,
∴2∈M,0∈M.
答案:A

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
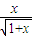 (x>0).
(x>0).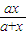 在(0,+∞)上单调递增,求实数a的取值范围.
在(0,+∞)上单调递增,求实数a的取值范围.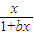
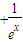 ≥1在[0,+∞)上恒成立,求实数b的最大值.
≥1在[0,+∞)上恒成立,求实数b的最大值.