题目内容
5.已知函数f(x)=x+ax-1(a>0).(Ⅰ)若f(1)=2且f(m)=5.求m2+m-2的值.
(Ⅱ)若f(x)在区间(1,+∞)上单调递增,求实数a的取值范围.
分析 (Ⅰ)由f(1)=2,得f(x)=x+x-1,从而f(m)=m+m-1=5,由此能求出m2+m-2.
(Ⅱ)由已知得当x∈(1,+∞)时,${f}^{'}(x)=1-\frac{a}{{x}^{2}}$>0恒成立,由此能求出实数a的取值范围.
解答 解:(Ⅰ)∵函数f(x)=x+ax-1(a>0),f(1)=2且f(m)=5.
∴1+a=2,解得a=1,∴f(x)=x+x-1,
∴f(m)=m+m-1=5,
∴m2+m-2=(m+m-1)2-2=25-2=23.
(Ⅱ)∵f(x)=x+ax-1(a>0)在区间(1,+∞)上单调递增,
∴当x∈(1,+∞)时,${f}^{'}(x)=1-\frac{a}{{x}^{2}}$≥0恒成立,
∴0<a≤1.
∴实数a的取值范围是(0,1].
点评 本题考查代数式的取值范围的求法,考查实数的取值范围的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
10.若α∈(0,π),且sinα+cosα=-$\frac{\sqrt{3}}{3}$,则α的取值范围是( )
| A. | (0,$\frac{π}{2}$) | B. | ($\frac{π}{2}$,π) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$) | D. | ($\frac{3π}{4}$,π) |
1.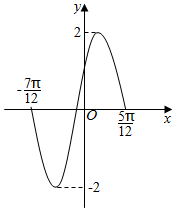 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则下列判断错误的是( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则下列判断错误的是( )| A. | A=2 | B. | ω=2 | C. | f(0)=1 | D. | φ=$\frac{5π}{6}$ |