Question

【题目】已知函数 （ ）在同一半周期内的图象过点 ， ， ，其中 为坐标原点， 为函数 图象的最高点， 为函数 的图象与 轴的正半轴的交点， 为等腰直角三角形.

（1）求 的值；
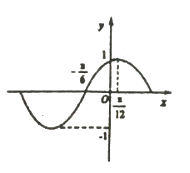
（2）将 绕原点 按逆时针方向旋转角 ，得到 ，若点 恰好落在曲线 （ ）上（如图所示），试判断点 是否也落在曲线 （ ）上，并说明理由.

Answer 1

【答案】
（1）解：因为函数 （ ）的最小正周期 ，所以函数 的半周期为 ，
所以 ，即有 坐标为 ，
又因为 为函数 图象的最高点，所以点 的坐标为 .
又因为 为等腰直角三角形，所以 .
（2）解：点 不落在曲线 （ ）上，理由如下：
由（1）知， ，
所以点 ， 的坐标分别为 ， .
因为点 在曲线 （ ）上，所以 ，即 ，又 ，所以 .
又 .所以点 不落在曲线 （ ）上.
【解析】（1）根据函数f（x）的解析式可得出其最小正周期为8，即半周期为4，故Q点的坐标为（4,0），P为最高点，解等腰直角三角形后可得P点坐标为（2,2）；（2）由（1）知，OP，OQ的大小，设出P ′ ， Q ′ 的坐标，根据点 P ′ 在曲线上得出等式，由三角恒等变换可sin2α，将 Q ′的坐标代入曲线方程，明显不满足.