题目内容
 如图,某农业研究所要在一个矩形试验田ABCD内种植三种农作物,三种农作物分别种植在并排排列的三个形状相同、大小相等的矩形中.试验田四周和三个种植区域之间设有1米宽的非种植区.已知种植区的占地面积为800平方米.
如图,某农业研究所要在一个矩形试验田ABCD内种植三种农作物,三种农作物分别种植在并排排列的三个形状相同、大小相等的矩形中.试验田四周和三个种植区域之间设有1米宽的非种植区.已知种植区的占地面积为800平方米.
(1)设试验田ABCD的面积为S,AB=x,求函数S=f(x)的解析式;
(2)求试验田ABCD占地面积的最小值.
解:(1)设ABCD的长与宽分别为x和y,
则(x-4)(y-2)=800
∴
(2)试验田ABCD的面积S=xy=
令x-4=t,t>0,则 ,
,
当且仅当 时,t=40,即x=44,此时,y=22.
时,t=40,即x=44,此时,y=22.
答:试验田ABCD的长与宽分别为44米、22米时,占地面积最小为968米2.
分析:(1))设ABCD的长与宽分别为x和y,则(x-4)(y-2)=800,由此能求出函数S=f(x)的解析式.
(2)试验田ABCD的面积S=xy= ,令x-4=t,t>0,则
,令x-4=t,t>0,则 ,由此能求出试验田ABCD占地面积的最小值.
,由此能求出试验田ABCD占地面积的最小值.
点评:本题考查函数问题在生产生活中的具体应用,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
则(x-4)(y-2)=800
∴

(2)试验田ABCD的面积S=xy=

令x-4=t,t>0,则
 ,
,当且仅当
 时,t=40,即x=44,此时,y=22.
时,t=40,即x=44,此时,y=22. 答:试验田ABCD的长与宽分别为44米、22米时,占地面积最小为968米2.
分析:(1))设ABCD的长与宽分别为x和y,则(x-4)(y-2)=800,由此能求出函数S=f(x)的解析式.
(2)试验田ABCD的面积S=xy=
 ,令x-4=t,t>0,则
,令x-4=t,t>0,则 ,由此能求出试验田ABCD占地面积的最小值.
,由此能求出试验田ABCD占地面积的最小值.点评:本题考查函数问题在生产生活中的具体应用,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
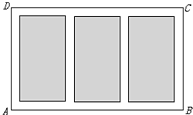 (2013•闸北区一模)如图,某农业研究所要在一个矩形试验田ABCD内种植三种农作物,三种农作物分别种植在并排排列的三个形状相同、大小相等的矩形中.试验田四周和三个种植区域之间设有1米宽的非种植区.已知种植区的占地面积为800平方米.
(2013•闸北区一模)如图,某农业研究所要在一个矩形试验田ABCD内种植三种农作物,三种农作物分别种植在并排排列的三个形状相同、大小相等的矩形中.试验田四周和三个种植区域之间设有1米宽的非种植区.已知种植区的占地面积为800平方米. (2013•闸北区一模)如图,某农业研究所要在一个矩形试验田ABCD内种植三种农作物,三种农作物分别种植在并排排列的三个形状相同、大小相等的矩形中.试验田四周和三个种植区域之间设有1米宽的非种植区.已知种植区的占地面积为800平方米,问:应怎样设计试验田ABCD的长与宽,才能使其占地面积最小?最小占地面积是多少?
(2013•闸北区一模)如图,某农业研究所要在一个矩形试验田ABCD内种植三种农作物,三种农作物分别种植在并排排列的三个形状相同、大小相等的矩形中.试验田四周和三个种植区域之间设有1米宽的非种植区.已知种植区的占地面积为800平方米,问:应怎样设计试验田ABCD的长与宽,才能使其占地面积最小?最小占地面积是多少?
