题目内容
F1、F2是双曲线C的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为( )
A、1+
| ||
B、2+
| ||
C、3-
| ||
D、3+
|
分析:先由△F1PF2是等腰直角三角形得|F1F2|=|PF2|,再把等量关系转化为用a,c来表示即可求双曲线C的离心率.
解答:解:由△PF1F2为等腰直角三角形,又|PF1|≠|PF2|,
故必有|F1F2|=|PF2|,即2c=
,
从而得c2-2ac-a2=0,即e2-2e-1=0,
解之得e=1±
,
∵e>1,∴e=1+
.
故选:A.
故必有|F1F2|=|PF2|,即2c=
| b2 |
| a |
从而得c2-2ac-a2=0,即e2-2e-1=0,
解之得e=1±
| 2 |
∵e>1,∴e=1+
| 2 |
故选:A.
点评:本题是对双曲线性质中离心率的考查.求离心率,只要找到a,c之间的等量关系即可求.是基础题.

练习册系列答案
相关题目
 (2013•南开区二模)如图,F1,F2是双曲线C:
(2013•南开区二模)如图,F1,F2是双曲线C: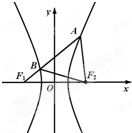 如图,F1,F2是双曲线C:
如图,F1,F2是双曲线C: