题目内容
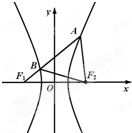 如图,F1,F2是双曲线C:
如图,F1,F2是双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| 7 |
分析:设△ABF2的边长为m,则由双曲线的定义,△ABF2为等边三角形,可求m的值,在△AF1F2中,由余弦定理,可得结论.
解答:解:设△ABF2的边长为m,则由双曲线的定义,可得|BF1|=m-2a
∴|AF1|=2m-2a
∵|AF1|-|AF2|=2a
∴2m-2a-m=2a
∴m=4a
在△AF1F2中,|AF1|=6a,|AF2|=4a,|F1F2|=2c,∠F1AF2=60°
∴由余弦定理可得4c2=(6a)2+(4a)2-2•6a•4a•
∴c=
a
∴e=
=
故答案为:
.
∴|AF1|=2m-2a
∵|AF1|-|AF2|=2a
∴2m-2a-m=2a
∴m=4a
在△AF1F2中,|AF1|=6a,|AF2|=4a,|F1F2|=2c,∠F1AF2=60°
∴由余弦定理可得4c2=(6a)2+(4a)2-2•6a•4a•
| 1 |
| 2 |
∴c=
| 7 |
∴e=
| c |
| a |
| 7 |
故答案为:
| 7 |
点评:本题考查双曲线的几何性质,考查余弦定理的运用,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
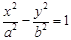 (a>0,b>0) 的左、右焦点,过F1的直线与
(a>0,b>0) 的左、右焦点,过F1的直线与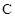 的左、右两支分别交于A,B两点.若 | AB | : | BF2
| : | AF2 |=3 : 4
: 5,则双 曲线的离心率为 .
的左、右两支分别交于A,B两点.若 | AB | : | BF2
| : | AF2 |=3 : 4
: 5,则双 曲线的离心率为 .