Question

【题目】已知函数f（x）=3mx﹣ ﹣（3+m）lnx，若对任意的m∈（4，5），x1 ， x2∈[1，3]，恒有（a﹣ln3）m﹣3ln3＞|f（x1）﹣f（x2）|成立，则实数a的取值范围是 ．

Answer 1

【答案】[ ，+∞）
【解析】解：函数的导数f′（x）=3m+ ﹣ =
= = ，
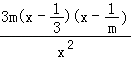∵m∈（4，5），
∴ ∈（ ， ），
由f′（x）＞0得x＞ 或x＜ ，此时函数单调递增，
由f′（x）＜0得 ＜x＜ ，此时函数单调递减，
∴当x∈[1，3]时，函数f（x）为增函数，
则函数的最大值为f（3）max=9m﹣ ﹣（3+m）ln3，
函数的最小值为f（1）min=3m﹣1，
则|f（x1）﹣f（x2）|max=9m﹣ ﹣（3+m）ln3﹣（3m﹣1）=6m+ ﹣（3+m）ln3，
则（a﹣ln3）m﹣3ln3＞|f（x1）﹣f（x2）|恒成立，
等价为（a﹣ln3）m﹣3ln3＞6m+ ﹣（3+m）ln3，
即am＞6m+ ，即a＞6+ ，
∵m∈（4，5），
∴ ∈（ ， ），
∴ ∈（ ， ），
则6+ ∈（ ， ），
则a≥ ，
即实数a的取值范围是[ ，+∞），
所以答案是：[ ，+∞）．