题目内容
3.若一等差数列前5项和为25,前10项和为100,则它的前15项的和为( )| A. | 125 | B. | 200 | C. | 225 | D. | 275 |
分析 由已知得S5,S10-S5,S15-S10成等差数列,由此能求出S15=120.
解答 解:由已知得S5,S10-S5,S15-S10成等差数列,
∵一个等差数列的前5项的和为25,前10项的和为100,
∴25,75,S15-100成等差数列,
∴25+S15-100=150,
解得S15=225.
故选:C.
点评 本题考查等差数列的前15项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
14.设△ABC的内角A,B,C所对边的长分别为a,b,c,若a:b:c=1:2:$\sqrt{7}$,则角C=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
8.y=$\frac{2}{x}$在区间[2,4]上的最大值、最小值分别是( )
| A. | 1,$\frac{1}{2}$ | B. | $\frac{1}{2}$,1 | C. | $\frac{1}{2}$,$\frac{1}{4}$ | D. | $\frac{1}{4}$,$\frac{1}{2}$ |
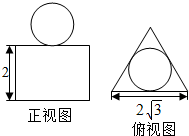 如图一个几何体的正视图和俯视图如图所示,其中俯视图为边长为2$\sqrt{3}$的正三角形,且圆与三角形内切,则该几何体的体积为$6\sqrt{3}+\frac{4π}{3}$.
如图一个几何体的正视图和俯视图如图所示,其中俯视图为边长为2$\sqrt{3}$的正三角形,且圆与三角形内切,则该几何体的体积为$6\sqrt{3}+\frac{4π}{3}$.