题目内容
如果偶函数 在
在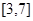 上是增函数且最小值是2,那么
上是增函数且最小值是2,那么 在
在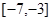 上是( )
上是( )
A.减函数且最小值是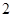 | B.减函数且最大值是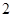 |
C.增函数且最小值是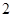 | D.增函数且最大值是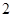 |
A
解析试题分析:根据偶函数的图像关于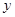 轴对称可知,偶函数在关于原点对称的区间,单调性相反且最值相同,所以依题意可知
轴对称可知,偶函数在关于原点对称的区间,单调性相反且最值相同,所以依题意可知 在
在 的单调性与在
的单调性与在 的单调性相反且有相同的最小值,所以
的单调性相反且有相同的最小值,所以 在
在 单调递减且最小值为2,故选A.
单调递减且最小值为2,故选A.
考点:1.函数的奇偶性;2.函数的单调性.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
定义在R上的函数 满足:
满足: 的图像关于
的图像关于 轴对称,并且对任意的
轴对称,并且对任意的
 有
有 ,则当
,则当 时,有( )
时,有( )
A. | B. |
C. | D. |
设偶函数 对任意
对任意 都有
都有 ,且当
,且当 时,
时, ,则
,则 ( )
( )
| A.10 | B. | C. | D. |
方程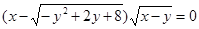 表示的曲线为 ( )
表示的曲线为 ( )
| A.一条直线和一个圆 | B.一条射线与半圆 |
| C.一条射线与一段劣弧 | D.一条线段与一段劣弧 |
已知 ,
, ,
, ,则( )
,则( )
A. | B. |
C. | D. |
 的零点个数为( )
的零点个数为( )
| A.4 | B.5 | C.6 | D.7 |
下列函数中,既是偶函数又在区间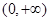 上单调递减的是__________.
上单调递减的是__________.
A.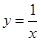 | B.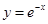 | C.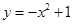 | D.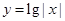 |
函数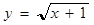 的定义域是( )
的定义域是( )
| A.(-¥,+¥) | B.[-1,+¥) | C.[0,+¥] | D.(-1,+¥) |
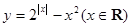 的图象大致为( )
的图象大致为( )