题目内容
椭圆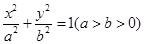 的右焦点
的右焦点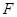 ,直线
,直线 与
与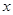 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点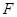 ,则椭圆离心率的取值范围是
,则椭圆离心率的取值范围是
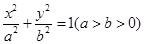 的右焦点
的右焦点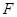 ,直线
,直线 与
与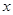 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点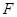 ,则椭圆离心率的取值范围是
,则椭圆离心率的取值范围是A.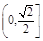 | B.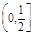 | C.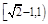 | D.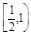 |
D
分析:由题意,椭圆上存在点P,使得线段AP的垂直平分线过点F,即F点到P点与A点的距离相等,根据|PF|的范围求得|FA|的范围,进而求得
 的范围即离心率e的范围.
的范围即离心率e的范围.解答:解:由题意,椭圆上存在点P,使得线段AP的垂直平分线过点F,即F点到P点与A点的距离相等
而|FA|=
 -c=
-c=
|PF|∈[a-c,a+c]
于是
 ∈[a-c,a+c]
∈[a-c,a+c]即ac-c2≤b2≤ac+c2
∴
 ,
,
又e∈(0,1)
故e∈[
 ,1].
,1].故选D.
点评:本题主要考查椭圆的基本性质,注意在解不等式过程中将
 看作整体,属基础题.
看作整体,属基础题.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
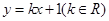 与椭圆
与椭圆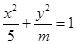 恒有公共点,则实数
恒有公共点,则实数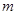 的取值范围为( )
的取值范围为( )
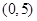
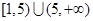
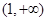
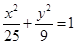 上一点M到焦点
上一点M到焦点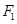 的距离为2,
的距离为2,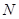 是
是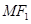 的中点,
的中点,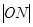 等于( *** )
等于( *** )
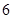
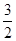
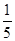

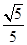
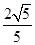
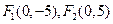 ,点
,点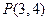
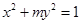 的离心率为
的离心率为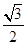 ,则它的长半轴长为( )
,则它的长半轴长为( ) (a>b>0)的离心率
(a>b>0)的离心率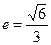 ,过点
,过点 和
和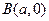 的直线与原点的距离为
的直线与原点的距离为
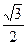 .
.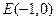 ,若直线
,若直线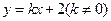 与椭圆交于
与椭圆交于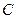 、
、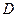 两点.问:是否存在
两点.问:是否存在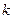 的值,使以
的值,使以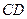 为直径的圆过
为直径的圆过 点?请说明理由.
点?请说明理由.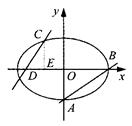
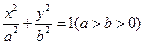 的左、右顶点,椭圆的长轴长为4,且点
的左、右顶点,椭圆的长轴长为4,且点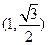 在该椭圆上。
在该椭圆上。 为锐角三角形
为锐角三角形 是椭圆
是椭圆 上的点,
上的点,  、
、 是椭圆的两个焦点,则
是椭圆的两个焦点,则 的值为( )
的值为( )