题目内容

6．若不等式mx2-mx+2＞0对一切实数x恒成立，则实数m的取值范围是（　　）
A．（0，8）B．[0，8]C．[0，8）D．（0，8]

分析 当m=0时，易知不等式恒成立，当m≠0时，可得$\left\{\begin{array}{l}{m＞0}\\{△=（-m）^{2}-4m•2＜0}\end{array}\right.$，从而解得．

解答 解：当m=0时，mx2-mx+2＞0可化为2＞0，成立；
当m≠0时，$\left\{\begin{array}{l}{m＞0}\\{△=（-m）^{2}-4m•2＜0}\end{array}\right.$，
解得0＜m＜8，
综上所述，
实数m的取值范围是[0，8），
故选C．

点评 本题考查了分类讨论的思想应用及恒成立问题的应用．

练习册系列答案
相关题目
16．已知圆C的标准方程为（x-5）2+（y-6）2=a2
（1）若点M（6，9）在圆上，求a的值；
（2）已知点P（3，3）和点Q（5，3）有一点在圆内，另一点在圆外，求a的取值范围．
17．已知集合A={1，2，3，4}，B={x|x=2n，n∈A}，则A∩B=（　　）
A．{1，4}B．{1，3}C．{2，4}D．{2，3}
14．已知集合P={x|x2-x-2≤0}，M={-1，0，3，4}，则集合P∩M中元素的个数为（　　）
A．1B．2C．3D．4
1．已知向量$\overrightarrow{a}$=（1，1），点A（3，0），点B为直线y=2x上的一个动点．若$\overrightarrow{AB}$∥$\overrightarrow{a}$，则点B的坐标为（-3，-6）．
11．已知函数f（x）=cos2x-sin2x，下列结论中错误的是（　　）
A．f（x）=cos2xB．f（x）的最小正周期为π
C．f（x）的图象关于直线x=0对称D．f（x）的值域为[-$\sqrt{2}$，$\sqrt{2}$]
18．已知x为实数，用[x]表示不超过x的最大整数，例如[1.2]=1，[-1.2]=2，[1]=1．对于函数f（x），若存在m∈R且m≠Z，使得f（m）=f（[m]），则称函数f（x）是Ω函数．
（Ⅰ）判断函数f（x）=x2-$\frac{1}{3}$x，g（x）=sinπx是否是Ω函数；（只需写出结论）
（Ⅱ）已知f（x）=x+$\frac{a}{x}$，请写出a的一个值，使得f（x）为Ω函数，并给出证明；
（Ⅲ）设函数f（x）是定义在R上的周期函数，其最小周期为T．若f（x）不是Ω函数，求T的最小值．
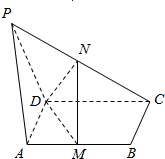15．如图，PA⊥平面ABCD，ABCD是矩形，M、N分别是AB，PC的中点．
（1）求证：MN⊥AB；
（2）若PA=AD，求证：平面MND⊥平面PDC．
16．已知M是△ABC内一点，且$\overrightarrow{AB}•\overrightarrow{AC}$=2$\sqrt{3}$，∠BAC=30°，若△MBC、△MAB、△MAC的面积分别为$\frac{1}{2}$、x、y．
（1）求△ABC的面积S的值；
（I2）求$\frac{1}{x}+\frac{4}{y}$的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网