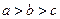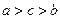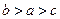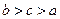题目内容
已知关于x的函数y=loga(2-ax)在[0,1]上是单调递减的函数,则a的取值范围为( )
| A.(0,1) | B.(1,+∞) | C.(0,2) | D.(1,2) |
∵关于x的函数y=loga(2-ax)在[0,1]上是单调递减的函数,
而函数t=2-ax在[0,1]上是单调递减的函数,
∴a>1 且函数t在[0,1]上大于零,故有
,
解得1<a<2,
故选:D.
而函数t=2-ax在[0,1]上是单调递减的函数,
∴a>1 且函数t在[0,1]上大于零,故有
|
解得1<a<2,
故选:D.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
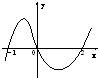
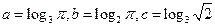 ,则
,则