题目内容
正实数x1,x2及函数f(x)满足 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值为( )
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值为( )A.4
B.2
C.

D.

【答案】分析:由已知须先求出f(x)的解析式 ,然后代入x1,x2及f(x1)+f(x2)=1可得含有入x1,x2的式子
,然后代入x1,x2及f(x1)+f(x2)=1可得含有入x1,x2的式子
 =
= ,再利用均值不等式求出
,再利用均值不等式求出 的范围,即可解答f(x1+x2)的最小值来.
的范围,即可解答f(x1+x2)的最小值来.
解答:解:由已知 得
得 ,由f(x1)+f(x2)=
,由f(x1)+f(x2)= +
+ =1
=1
于是可得: ,
,
所以得: =
= ≥2
≥2 ,①
,①
设 =t,则①式可得:t2-2t-3≥0,又因为t>0,
=t,则①式可得:t2-2t-3≥0,又因为t>0,
于是有:t≥3或t≤-1(舍),从而得 ≥3,即:
≥3,即: ≥9,
≥9,
所以得:f(x1+x2)= =
= =
= ≥1-
≥1- =
= .
.
所以有:f(x1+x2)的最小值为 .
.
故应选:C
点评:本题考查函数最值的求法,指数函数的性质,函数解析式的运算,指数的运算,均值不等式的应用,考查的思想方法较综合,考查学生的运算能力要求较强.
 ,然后代入x1,x2及f(x1)+f(x2)=1可得含有入x1,x2的式子
,然后代入x1,x2及f(x1)+f(x2)=1可得含有入x1,x2的式子 =
= ,再利用均值不等式求出
,再利用均值不等式求出 的范围,即可解答f(x1+x2)的最小值来.
的范围,即可解答f(x1+x2)的最小值来.解答:解:由已知
 得
得 ,由f(x1)+f(x2)=
,由f(x1)+f(x2)= +
+ =1
=1于是可得:
 ,
,所以得:
 =
= ≥2
≥2 ,①
,①设
 =t,则①式可得:t2-2t-3≥0,又因为t>0,
=t,则①式可得:t2-2t-3≥0,又因为t>0,于是有:t≥3或t≤-1(舍),从而得
 ≥3,即:
≥3,即: ≥9,
≥9,所以得:f(x1+x2)=
 =
= =
= ≥1-
≥1- =
= .
.所以有:f(x1+x2)的最小值为
 .
.故应选:C
点评:本题考查函数最值的求法,指数函数的性质,函数解析式的运算,指数的运算,均值不等式的应用,考查的思想方法较综合,考查学生的运算能力要求较强.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .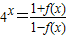 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值为( )
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值为( )

 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值= .