题目内容
1.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且短轴长为2,F1,F2是左右焦点,O为坐标原点.(1)求椭圆的标准方程;
(2)圆O是以F1,F2为直径的圆,直线l:y=kx+m与圆O相切,且与椭圆交于A,B两点,$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{2}{3}$,求k的值.
分析 (1)短轴长2b=2,即b=1,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a2=b2+c2,解得:a=$\sqrt{2}$,b=1,即可求得椭圆的标准方程;
(2)以F1,F2为直径的圆,x2+y2=1,由直线l:y=kx+m与圆O相切,则$\frac{丨m丨}{\sqrt{1+{k}^{2}}}$=1,即m2=1+k2,将直线l代入椭圆方程,利用韦达定理及向量数量积的坐标运算即可求得:$\frac{1+{k}^{2}}{1+2{k}^{2}}$=$\frac{2}{3}$,即可求得k的值.
解答 解:(1)椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)焦点在x轴上,短轴长2b=2,即b=1,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
又a2=b2+c2,解得:a=$\sqrt{2}$,b=1,
∴椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)由(1)可知:丨F1F2丨=2c=2,则以F1,F2为直径的圆,x2+y2=1,
由直线l:y=kx+m与圆O相切,则$\frac{丨m丨}{\sqrt{1+{k}^{2}}}$=1,即m2=1+k2,
设A(x1,y1),B(x2,y2)
由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,消去y得,(1+2k2)x2+4mkx+2m2-2=0,
由直线与椭圆有两个不同的交点,
即有△>0,即(4km)2-4(1+2k2)(2m2-2)>0,
解得:k2>0,
又x1+x2=-$\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-2}{1+2{k}^{2}}$,
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=$\frac{1-{k}^{2}}{1+2{k}^{2}}$,
则$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=$\frac{2{m}^{2}-2}{1+2{k}^{2}}$+$\frac{1-{k}^{2}}{1+2{k}^{2}}$=$\frac{1+{k}^{2}}{1+2{k}^{2}}$=$\frac{2}{3}$,解得:k=±1.
∴k的值±1.
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,考查向量数量积的坐标运算,韦达定理的应用,考查计算能力,属于中档题.

| A. | ∅ | B. | {1,2} | C. | [0,3) | D. | {0,1,2} |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
| A. | ?x0∈R,x02+sinx0+e${\;}^{{x}_{0}}$>1 | B. | ?x0∈R,x02+sinx0+e${\;}^{{x}_{0}}$≥1 | ||
| C. | ?x∈R,x2+sinx+ex>1 | D. | ?x∈R,x2+sinx+ex≥1 |
| A. | 1 | B. | -1 | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
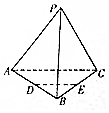 如图,在正三棱锥P-ABC中,D,E分别是AB,BC的中点.
如图,在正三棱锥P-ABC中,D,E分别是AB,BC的中点.